|
Historias matemáticas - 2 |
|
|
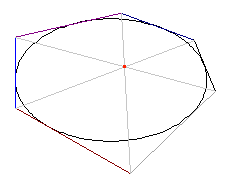
El principio de dualidad: los teoremas de Pascal y BrianchonEl principio de dualidadEn el plano euclídeo habitual es evidente que dos puntos definen una recta, justo aquella que los contiene. Al revés, sin embargo, no es cierto, pues dos rectas, además de cortarse y definir por tanto un punto, también pueden ser paralelas. Esta excepción desaparece en el caso del plano proyectivo, pues en él, por definición, cada haz de rectas paralelas define un punto del infinito, por lo que se dice aquello de que las rectas paralelas se cortan "en el infinito". La completa simetría de estas dos proposiciones ("dos puntos definen una recta", "dos rectas definen un punto") en el plano proyectivo es la base del principio de dualidad, truco genial por el cual todo lo que se dice de los puntos puede decirse de las rectas, y al revés (esta simetría puede entenderse si pensamos que para situar un punto en el plano se necesitan dos números, sus coordenadas, y para situar una recta, igualmente dos números: su pendiente y su ordenada en el origen). Veamos la potencia del principio de dualidad con un ejemplo: Teorema de Pascal Estamos en los años treinta del siglo XVII. El joven Pascal acudía, acompañando a su padre, a las reuniones matemáticas organizadas en París por Mersenne, y allí quedó fascinado por los trabajos de Desargues. Producto de esta fascinación, hacia 1639 y con tan solo dieciseis años, Pascal demostró el teorema que ahora lleva su nombre (él lo llamó mysterium hexagrammicum) y que afirma que los seis vértices de un hexágono están sobre una cónica si y solo si los tres puntos comunes a los tres pares de lados opuestos están en una recta común (ojo: estamos en el plano proyectivo, de modo que si dos rectas son paralelas el punto común será un punto del infinito).
A partir de este teorema Pascal demostraría del orden de 400 teoremas y corolarios. Es de señalar que ni en el enunciado ni en la demostración del teorema aparece en ningún momento magnitud alguna de ángulos o segmentos, lo cual es suficiente, como dijo E. T. Bell, "para abolir la estúpida definición de las matemáticas [...] como ciencia de la 'cantidad'". La proyectividad del teorema se ve fácilmente si pensamos en el esquema como la sección de un cono mediante un plano. Si después, sobre el mismo cono, realizamos otra sección, la proyección de todos los elementos (puntos, rectas, la propia cónica) compondrá otro mysterium hexagrammicum. Teorema de Brianchon Seguimos en Francia, pero más de siglo y medio después, y con otro joven, esta vez de veintiún años, Charle Julien Brianchon, estudiante de la École Polytechique, donde en 1806 publicaría su teorema, que afirma que los seis lados de un hexágono son tangentes a una cónica si y solo si las tres rectas que unen los tres pares de vértices opuestos tienen una punto común.
Si comparamos los esquemas de los teoremas de Pascal y Brianchon puede que no encontremos demasiadas semejanzas. Sin embargo, gracias a la geometría proyectiva y al principio de dualidad, podemos ver que son completamente equivalentes: si en el enunciado del teorema de Pascal sustituimos 'punto' por 'recta' y 'recta' por 'punto' y consideramos que una recta 'está sobre una cónica' cuando es 'tangente a la cónica', obtenemos sorprendentemente el teorema de Brianchon: "Los seis vértices/lados de un hexágono están sobre una cónica si y solo si los tres puntos/rectas comunes a los tres pares de lados/vértices opuestos tienen una recta/punto común." Este par de teoremas no son solo centrales en el estudio proyectivo de las cónicas, sino que constituyen el primer ejemplo claro en geometría, dice Boyer, de dos teoremas duales. Sin embargo, sería otro francés, contemporáneo de Brianchon, y considerado como el padre de la geometría proyectiva, quién explotaría con efectividad el principio de dualidad: Poncelet. Men of mathematics, pp.78, 216; Boyer, pp.454, 657. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
La Torre de HanoiEn 1883, el matemático francés Édouard Lucas d’Amiens publicó un problema bajo el pseudónimo de N. Claus de Siam que, sin embargo, perduraría en la legendaria forma que le dio De Parville al año siguiente:"Él refirió que en el gran templo de Benarés, debajo de la cúpula que marca el centro del mundo, yace una base de bronce en la que se encuentran fijadas tres agujas de diamante de una codo de altura y del grueso del cuerpo de una abeja. En una de estas agujas, Dios, en el comienzo de los siglos, colocó sesenta y cuatro discos de oro puro, el mayor sobre el plato de bronce, y los otros, en orden decreciente de anchura, superpuestos hasta la cima. Esta es la Torre de Brahma. Día y noche, los sacerdotes se turnan en la ocupación de transportar la torre de la primera aguja de diamante a la tercera, sin desviarse de las reglas fijas e inmutables impuestas por Brahma. El sacerdote no debe mover más de un disco a la vez; y no debe colocar un disco más que en una aguja libre o sobre un disco mayor. Cuando siguiendo estrictamente estas recomendaciones los sesenta y cuatro discos hayan sido transferidos de la aguja en la que Dios los colocó a la tercera, la torre y los brahmanes se convertirán en polvo y será el fin del mundo." (*). Dicho esto, es evidente que a todos nos interesará saber cuándo finalizarán los sacerdotes su tarea para hacernos una idea del tiempo que nos queda. Afortunadamene, el número de pasos se puede calcular fácilmente por inducción:
Si los brahmanes fuesen capaces de realizar una trasferencia cada segundo (que ya es transferir), el tiempo necesario para trasladar la columna sería, aproximadamente, de 585.000.000.000 años, que viene a ser más de cien veces la edad actual de nuestro sol, lo cual es suficientemente tranquilizador, al menos en lo que respecta al problema que nos ocupa: ya encontraremos otro modo de acabar con el mundo. En un cuento de Arthur C. Clarke titulado Los nueve mil millones de nombres de Dios (The Nine Billion names og God) se cuenta una historia parecida: unos monjes tienen la tarea de escribir mediante combinaciones de ciertos caracteres especiales todos los posibles nombres de Dios, unos nueve mil millones, tarea que según sus propios cálculos les mantendría ocupados durante unos quince mil años. La cosa es que han pensado que utilizando ordenadores podrían acortar ese tiempo a unos mucho más razonables tres meses, por lo que alquilan un equipo de programadores y un ordenador Mark V para que lleve a cabo la tarea. Lo que no saben los operarios del ordenador es que, según las creencias de los monjes, cuando todos los nombres de Dios hayan sido escritos el mundo desaparecerá... (*) Fuentes:
Historias matemáticas: Triángulo de Sierpinsky |
||||||||||||||||||||||||||||||||||||||||||||||||||||
Teorema de DesarguesDesargues, contemporáneo de Descartes, basándose en la perspectiva pictórica renacentista y en el principio de continuidad de Kepler, llevó a cabo un estudio auténticamente revolucionario de las cónicas. Su idea central consistió en estudiar aquellas propiedades de los objetos geométricos que permanecen invariantes bajo proyección. De esta manera, las cónicas resultan una familia "estrechamente unida". Sin embargo, los tiempos no estaban lo suficientemente maduros para esta nueva geometría proyectiva, entre otras cosas por el furor que causó el estudio algebraico de la geometría de Descartes, y Desargues sería recordado casi exclusivamente por el siguiente teorema, que lleva su nombre: Teorema: Si dos triángulos ABC y A'B'C' son de tal forma que las rectas AA', BB' y CC' se cortan en un único punto O, entonces los puntos de intersección de las rectas AB y A'B', AC y A'C', BC y B'C' (P, Q y R respectivamente) están alineados. Es particularmente interesante la demostración del teorema, pues muestra espectacularmente la potencia de la geometría proyectiva: en vez de considerar los dos triángulos inmersos en el mismo plano, se puede considerar que lo que estamos viendo en realidad es la proyección plana de un sistema tridimensional en el que el segundo triángulo es la proyección del primero desde el punto O en un plano no paralelo al del primero. Al no ser paralelos, los dos planos se cortarán en una recta. Esta recta contendrá las intersecciones de los lados correspondientes. Listo. Nota. el esquema, si no lo has descubierto ya, es interactivo: prueba a mover cualquiera de los puntos de los triángulos o alguna de las rectas OA, OB, OC: verás que los puntos P, Q y R se mantiene alineados.
***
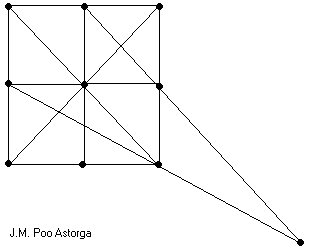
Un problema: Diez árboles en diez filas de tres Un viejo problema dice: ¿Cómo plantar diez árboles en diez filas de tres árboles cada una de modo que cada árbol esté exactamente en tres filas? Hay que tener en cuenta que no se da ninguna condición sobre las filas, ni en cuanto a su paralelismo ni en cuanto a su longitud. Sin embargo, pese a todas las libertades, resolver el problema no resulta nada fácil (reto al lector a que lo intente)... a no ser que uno conozca el teorema de Desargues. En este caso, la cuestión resulta trivial, pues una inspección del esquema dado nos da la solución: basta colocar los árboles en los puntos A, B, C, A', B', C', P, Q, R y O. To Infinity and Beyond, p.113; Boyer, p.452. Nota: en un principio, un servidor escribió el siguiente enunciado: ¿Cómo plantar diez árboles en diez filas de tres árboles cada una?, que tuve que corregir cuando José (12-11-2003) mandó la siguiente solución, obtenida por un compañero de clase:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
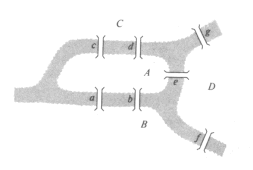
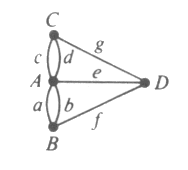
Los siete puentes de KönigsbergEl río Pregel, a su paso por la ciudad alemana de Königsberg (hoy Königsberg es rusa y se llama Kaliningrado), forma dos islas. En el siglo dieciocho ambas islas estaban conectadas entre sí y con las dos orillas del río mediante siete puentes. Se dice que sus habitantes intentaron durante años encontrar un camino que cruzase cada puente una y solo una vez y que volviese al punto de partida. Nunca lo encontraron. La cuestión era: ¿existe tal camino?El problema fue resuelto por Euler en una memoria que presentó en 1735 en la Academia de San Petersburgo. Trataba el tema en una forma mucho más general, de modo que resolvía el problema de los siete puentes como un caso particular. Supuso el inicio de la teoría de grafos y el comienzo de la topología, un nuevo tipo de geometría menos preocupado por lo cuantitativo y más por las propiedades cualitativas de las formas.
La idea básica de su razonamiento es de una sencillez pasmosa: para cumplir con las condiciones del problema, si uno llega a un nodo a través de una arista, debe salir de él por una arista distinta, lo que nos lleva a que en cada nodo el número de aristas que llegan a él debe ser par, cosa que en el caso de los puentes de Königsberg no es cierta: a los nodos B, C y D llegan tres aristas, mientras que al nodo A llegan cinco. Así de sencillo. Así de genial. Mathematical Recreations and Essays, p.243; Matemáticas e imaginación, p.262; Dances with Dodecahedra, p.86. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
El problema de los conejosEn 1202, Leonardo de Pisa, más conocido como Fibonacci, publica su famoso Liber Abaci, en el que explica y recomienda la utilización de los numerales indo-arábigos. Entre los problemas que plantea hay uno de apariencia inocente que dice: ¿Cuántas parejas de conejos se producirán en un año, comenzando por una pareja única, si cada mes cualquier pareja engendra otra pareja, que se reproduce a su vez desde el segundo mes? Su solución puede consistir en una tabla como la siguiente:
La importancia de este problema reside en ser el punto de arranque de la más famosa de las sucesiones: si se observa la fila titulada "total parejas" veremos que cada término a partir del tercero es igual a la suma de los dos anteriores. Pues bien, a la sucesión definida por recurrencia de esta manera se le llama sucesión de Fibonacci, y de ella se han encontrado desde entonces multitud de sorprendentes e interesantes resultados. De ello puede dar idea el número de veces que aparece citada en este sitio o el que exista una asociación dedicada a su estudio, "The Fibonacci Association", cuyos trabajos se editan en la revista "The Fibonacci Quarterly". Sin duda, una de las razones de su éxito radica en su estrecha relación con la razón áurea. Boyer, p.329; Britannica ('Fibonacci numbers'). |