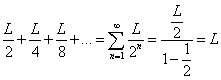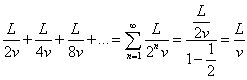Índice |
 |
||||||||
Paradoja de los catálogosSupongamos que el bibliotecario de la Biblioteca de Babel, al ver que la cantidad da catálogos que pueblan las estanterías, decide poner un poco de orden. Como observa que algunos catálogos se mencionan a sí mismos (por ejemplo, el catálogo de los catálogos) y otros no (como el catálogo de los peces, pues un catálogo no es un pez) decide componer el catálogo de los catálogos que no se mencionan a sí mismos. Todo va bien hasta que el bibliotecario se pregunta si su nuevo catálogo debe mencionarse a sí mismo o no. Ficciones: La Biblioteca de Babel, p.89; Conceptos de matemática moderna, p.324. |
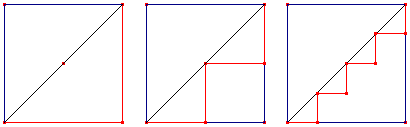
La diagonal escalonada (2 = raíz de 2)
Si vamos por una escalera de un vértice a otro de un cuadrado (que suponemos de lado unidad), da igual el número de peldaños que le pongamos: la escalera siempre medirá 2 unidades. Por otra parte, aumentando el número de peldaños, podemos acercarnos tanto como queramos a la diagonal. Dicho de otra manera: podemos construir una sucesión, la de las escaleras con un número creciente de peldaños, cuyos terminos valen todos 2, que tiende, sin embargo, a la diagonal, que mide raíz de 2. Conclusión, El reto de Hilbert, p.144; Éste es el tiempo del mundo finito, p.42. |
La moda de la originalidadEn los años que vivimos la busca de la originalidad se ha convertido, entre los escritores, los artistas y sus adláteres, en un auténtico movimiento de masas, o dicho simplemente, en una moda, que es la negación de la originalidad. ABC de Adolfo Bioy Casares, p.35. |
La paradoja del tesoroLe dijo el estafador a su víctima que podría recoger el tesoro prometido en un cierto lugar en la noche de San Juan a condición de que mientras cavase no pensase en un cocodrilo blanco, porque en tal caso el tesoro desaparecería. Art & Illusion, p.150. |
Clases de personas
Notas:
|
Grandes modestos¿Comprendéis ahora por qué los grandes hombres solemos ser modestos? Antonio Machado, Juan de Mairena, p.103. |
Demostración de que 2 = 1
¿Dónde está el error de esta "demostracion"? Enviada por Alberto Alcocer el 12-7-2004. Solución:
Calculus, p.17. Otra variante en Chistes: El día que abandoné ingeniería. |
Hotel de HilbertHilbert imaginó un hotel con infinitas habitaciones numeradas 1, 2, 3, 4... Un noche que estaba el hotel completamente ocupado llegó un cliente pidiendo una habitación. El gerente, que en sus ratos libres se dedicaba a las matemáticas, no vio problema ninguno: hizo que cada cliente se moviese a la habitación siguiente, de modo que el de la habitación 1 pasase a la 2, el de la 2 a la tres, y así sucesivamente, de modo que todo el mundo quedó alojado y la habitación 1 libre para el recién llegado. Al día siguiente la situación fue aún más complicada, pues llegó un autocar con infinitos turistas necesitados de habitación. El gerente, que no se arredraba ante nada, hizo que el ocupante de la habitación 1 pasase a la 2, el de la 2 a la 4, el de la 3 a la 6, y así sucesivamente según la regla n ► 2n, de modo que todas las habitaciones impares quedaron disponibles para los nuevos huéspedes. De aquí al infinito, p.70. |
Paradoja de GalileoLlamenos cuadrados a aquellos números que se obtienen multipicando un numero natural por sí mismo: 1, 4, 9... A los números que los generan los llamaremos raíces. Así, 1 es raíz de 1, 2 de 4, 3 de 9...
Conclusión: hay tantos cuadrados como números en total, lo cual es paradógico, pues no todos los números son cuadrados. De hecho, cuanto mayores son los números, menor es la cantidad de cuadrados. Por ejemplo, del primer millón de números, solo mil son cuadrados. Diálogo sobre dos nuevas ciencias, p.376. |
Paradoja de la dicotomíaSe supone comúnmente que un atleta puede desplazarse desde el punto de salida (A) hasta la meta (B). Sin embargo, según Zenón, esto es imposible. Su argumento es el siguiente: antes de llegar a la meta el atleta deberá recorrer la mitad de la distancia y alcanzar el punto medio de A y B, esto es, I1. Alcanzado el punto I1, antes de llegar a B deberá recorrer la mitad de la distancia que le queda y alcanzar el punto medio de I1 y B, esto es, I2. Continuando el argumento indefinidamente, el corredor deberá, antes de llegar a B, recorrer infinitos trayectos en un tiempo finito, lo cual es imposible. En este argumento Zenón asume que el espacio es continuo y, por tanto, infinitamente divisible. Sin embargo, no hace lo mismo con el tiempo, lo que da lugar a la paradoja. Veamos primero qué es lo que hace con el espacio: Suposición: el espacio es infinitamente divisible Aunque pueda resultar sorprendente en un principio, es posible sumar infinitas cantidades y que el resultado sea finito. Un ejemplo sencillo es el de las progresiones geométricas, que son aquellas sucesiones en las que cada término se obtiene multiplicando al anterior por una cantidad constante llamada razón. Si dicha razón es menor que uno es fácil demostrar que la suma de los infinitos términos de la progresión se obtiene mediante la fórmula S = a1/(1 - r), donde a1 es el primero de los términos. Un caso especialmente intuitivo es el de la progresión 1/2, 1/4, 1/8, 1/16, 1/32... Parece claro que si primero cogemos la mitad de la unidad, y luego la mitad de lo que queda, y luego la mitad de lo que queda, y así "hasta el infinito", acabaremos cogiendo la unidad completa:
Efectivamente: aplicando la fórmula anterior para la suma, se tiene:
El caso planteado por Zenón es esencialmente el mismo: supongamos que la distancia a recorrer es L. Entonces los intervalos a recorrer por el atleta serán L/2, L/4, L/8..., cantidades que resultan ser los términos de una progresión geométrica de razón 1/2 cuya suma es:
Es decir, que no hay problema en subdividir el espacio infinitamente. ¿Y el tiempo? Si la velocidad del atleta es v (que consideramos constante por comodidad), el tiempo que tardará en recorrer el primer intervalo será L/2v, y el segundo L/4v, y así sucesivamente. Zenón en este punto dice que el corredor nunca podrá llegar a la meta porque recorrer los infinitos intervalos le llevaría un tiempo infinito. Pero se equivoca: si sumamos todos los tiempos, tenemos:
que es una cantidad de tiempo finita. Conclusión A no ser que alguna razón nos lo impida, si aceptamos la continuidad del espacio debemos aceptar la del tiempo, lo cual nos autoriza a recorrer infinitos intervalos espaciales en un tiempo finito. Conviene indicar que los cálculos anteriores no demuestran que el movimiento sea posible, sino que el argumento de Zenón no es correcto. El mundo físico Hasta ahora hemos hablado en términos puramente matemáticos. Pero, ¿y qué dice la física? Pues dice que aunque no conozcamos la microestructura detallada del espacio-tiempo sí que sabemos que no puede ser cortado ilimitadamente. Para observar un detalle necesitamos una longitud de onda menor que el detalle mismo. Para que la longitud de onda sea menor debe aumentarse la energía, pero esto puede hacerse tan solo hasta cierto límite, pues alcanzado este la concentración de energía llevaría a un agujero negro. La longitud a la que ocurre esto, la mínima posible, es la conocida como longitud de Plank. El tiempo de Plank es el que tarda la luz en cruzar esa distancia. Dado que nada viaja más rápido que la luz, este es el tiempo mínimo posible. Por debajo de esa distancia y ese tiempo nada se puede observar y la realidad deja de tener sentido. De ser esto cierto (no olvidemos que estamos hablando de física y, por tanto, de teorías), nos encontraríamos en un espacio-tiempo discreto y la paradoja de Zenon se desvanecería automáticamente pues, como se ha visto, el argumento de Zenon parte de la suposición de un espacio infinitamente divisible. Una variante Antes de llegar al punto medio de A y B, esto es, I1, el corredor debería llegar al punto medio de A e I1, esto es, I2. Y antes de llegar a I2 debería de llegar al punto medio de A e I2, esto es, I3. Repitiendo el proceso indefinidamente sumimos al corredor en una extraña inmovilidad, pues antes de alcanzar cualquier punto de la trayectoria debe haber pasado por una cantidad infinita de ellos. El tema de las paradojas de Zenon fue sugerido por Diana. Después DrGEN sugirió hablar de los límites físicos del espacio-tiempo. Bibliografía: |
Zaratustra: poeta y mentiroso"Sin embargo, ¿qué te dijo en otro tiempo Zaratustra? ¿Que los poetas mienten demasiado? - Mas también Zaratustra es un poeta." Así habló Zaratustra, p.189. |
Paradoja del mentiroso o de EpiménidesDijo el cretense Epímenides allá por el siglo VI. a.n.e: "Los cretenses, siempre embusteros". La Biblia, Epístola a Tito, v. 12. En realidad esto no es exactamente una paradoja, pues existe una posibilidad coherente, y es que Epiménides mintiese cuando dijo "Los cretenses, siempre embusteros". Para que sea una auténtica paradoja, hay que añadir como premisa que todas las demás afirmaciones de los cretenses son falsas. Desde un punto de vista lógico, p.192. |
Paradoja de la tarjetaEl matemático P.E.B. Jourdain, en 1913, propuso la siguiente paradoja: en uno de los lados de una tarjeta se podía leer:
En la otra cara estaba escrito:
Orden y sorpresa, p.74. |
Paradoja del barberoPropuesta por Bertrand Russell, dice: El único barbero de la ciudad dice que afeitará a todos aquellos que no se afeiten a sí mismos. Pregunta: ¿quién afeitará al barbero? Si no se afeita a sí mismo será una de las personas de la ciudad que no se afeitan a sí mismas, con lo cual debería de afeitarse, siendo por tanto una de las personas que se afeitan a sí mismas, no debiendo por tanto afeitarse. Imposibilidad, p.42. |
Paradoja de los alcaldesÉrase una vez un reino donde había muchas ciudades y por tanto muchos alcaldes. Algunos alcaldes vivían en la ciudad que gobernaban y otros no. El rey, a fin de tener controlados a los alcaldes, decidió que eso se terminaría, y que los alcaldes no podrían vivir donde les pareciera. Lo que hizo fue construir una ciudad que llamó ZAD (Zona de Alcaldes Desplazados) y decretó que en ella vivirían únicamente los alcaldes que no viveran en la ciudad que governaban. Pronto surgió un problema. ¿Dónde debería el rey mandar a vivir al alcalde de la nueva ciudad? Ulises nos manda esta versión de paradoja autorreferencial. Su fuente es el libro de John Allen Paulos Más allá de los números. |
Paradoja de RussellLos conjuntos parecen ser de dos tipos: los que se contienen a sí mismos como miembros y los que no. Un ejemplo de los primeros sería el conjunto de las cosas pensables, pues a su vez es una cosa pensable. Un ejemplo de los segundos sería el conjunto de los matemáticos, pues el conjunto en sí no es un matemático y, por tanto, no pertenece al conjunto como miembro. Consideremos ahora el conjunto todos los conjuntos que no se contiene a sí mismos como miembro. Llamémosle T. ¿está T contenido en sí mismo como miembro? Si lo está, por definición no se contiene a sí mismo, luego no lo está. Pero si no lo está, por definición, debe estar. El teorema de Gödel, p.40; ¿Qué son y para qué sirven los números?, p.66. |
Paradoja de GrellingLos adjetivos se pueden clasificar en autodescriptivos (los que se pueden aplicar a sí mismo) y no-autodescriptivos. Polisilábico, corto, castellano son autodescriptivos (el adjetivo polisilábico tiene más de dos sílabas, luego es polisilábico), mientras que monosilábico, largo y alemán son no-autodescriptivos. Consideremos el adjetivo no-autodescriptivo: ¿es autodescriptivo o no-autodescriptivo? Orden y sorpresa, p.77. El nombre le viene por el matemático alemán Kurt Grelling. |
El pleito sobre los honorariosLa paradoja lógica que voy a relatar se le planteó al filósofo griego Protágoras hace unos 2.400 años aproximadamente. Protágoras fue uno de los precursores del movimiento sofista. Según algunos de sus contemporáneos fue el primero que sostuvo que sobre una misma cuestión existen dos discursos mutuamente opuestos. Durante años enseñó sus conocimientos a los hijos de las familias pudientes griegas, por los que cobró grandes sumas de dinero. Los cursos eran rápidos y eficaces, y entre las enseñanzas transmitidas gran parte la ocupaban tanto la retórica como la argumentación. Para que os hagáis una idea, las escuelas sofistas eran, en aquél entonces, lo que hoy pueden ser las universidades privadas. Las enseñanzas de los sofistas eran muy valiosas para aquellos que quisieran hacer carrera política o judicial. El pleito de los honorarios se plantea entre el maestro Protágoras y su discípulo Evatlo al que acoge en su academia con la condición de que le pagara los honorarios del curso cuando ganase su primer pleito. Terminado el curso Evatlo no tuvo ningún cliente y Protágoras, que era sofista pero no estoico, demandó a su discípulo. Los argumentos expuestos fueron los siguientes: Evatlo: Tanto si gano como si pierdo, en ningún caso tendré obligación de pagar a Protagoras. Si yo gano el pleito no tendré que pagar ya que el Juez habrá desestimado la demanda. Si lo pierdo, entonces, no habré ganado mi primer pleito y por lo tanto no se habrá cumplido la condición que hacía exigible la obligación de pago de los honorarios. Protágoras: Tanto si gano como si pierdo este pleito, Evatlo siempre tendrá obligación de pagarme. Si yo gano la demanda, por definición tendrá que pagarme pues esta es la cuestión que se ventila en este pleito. Y si la pierdo, también tendrá que pagarme porque significará que ha ganado su primer pleito; es decir se habrá cumplido la condición de nuestro acuerdo. ¿Quién creéis que tenía razón? Juan Carlos manda esta paradoja (24-8-2003) y dice: "La paradoja la recoge Raymond Smullyan. He añadido algunos datos que aparecen en el libro Sofistas, Testimonios y Fragmentos de la Editorial Gredos". El origen de la paradoja reside en el hecho de que tanto Protágoras como su alumno primero aceptan la autoridad del tribunal pero después, si el veredicto no les favorece, deciden no someterse. Dicho de otra manera: más que una paradoja este es un caso de mala fe por parte de maestro y alumno. La finalidad del pleito es resolver el conflicto entre las partes. Pero deja de tener sentido si dichas partes condicionan su acatamiento al resultado. Conclusión: Si no van a jucicio, pues no hay paradoja. Si van a jucicio, tendrán que acatar lo que decida el tribunal y listo. Paradox Lost |

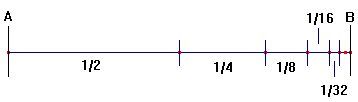
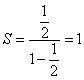 .
.