Aritmética

1. La suma de tres números enteros positivos desconocidos es 12. Hallar el número más pequeño que se puede obtener multiplicando estos tres números

2. Suponemos que todo número de siete dígitos es un posible número telefónico, excepto si comienza con 0 ó ¿Cuál es la fracción de números telefónicos que comienzan con 9 y terminan con 0?

3. A y B son dos números enteros diferentes escogidos entre 1 y 40 inclusive. ¿Cuál es el mayor valor que puede tomar la siguiente expresión?

4. La suma de seis números es par, el producto de los cuatro primeros es impar y el último es par. ¿El quinto número es par o impar?

5. Carlos tiene un cierto número de monedas de colección. Cuando ordena las monedas en montones de 5, no le sobra ninguna moneda. Cuando las ordena en montones de a 6, tampoco le sobran monedas. Pero si las ordena en montones de 7, le sobra una moneda. ¿Cuál es el menor número de monedas que puede tener Carlos?

6. ¿Cuáles son las últimas dos cifras de 2 ²²² ?

7. Los números a partir de 1 son colocados en cuatro columnas como se muestra en el dibujo. ¿En que columna y en que fila debe aparecer el número 1997?

8. ¿Cuál es el menor número natural por el que debemos multiplicar 504 para obtener un cuadrado perfecto?

9. Se sabe que el producto de tres números enteros positivos es 180. Si se sabe que dos de los números son iguales, ¿cuál es el menor valor que puede tomar la suma de los tres números?

10. ¿De cuántas maneras se puede escribir el número 7800 como producto de dos factores enteros positivos?

11. Probar que el número abcabc es múltiplo de 7, de 11 y de 13.

12. Probar que ninguno de los enteros 1573, 15731573, 157315731573, etc., es un número primo.

13. Determine todos los pares de números que tienen el mismo máximo común divisor y mínimo común múltiplo que el par de números 1470 y 126.

14. Hallar un número de 3 cifras ab6 sabiendo que las tres últimas cifras de ( ab6)² son ab6.

15. Un número de 5 cifras que termina en 7 se pasó 4 números de un capicúa y le faltan 7 números para el siguiente capicúa (Un número capicúa es aquel que se lee igual de izquierda a derecha y viceversa, por ejemplo: 4093904). ¿Qué número es?

16. En la multiplicación de la derecha, cada una de las letras A, B y C representan dígitos. Las rayas representan dígitos distintos de 0. ¿Cuáles son los dígitos que representan las letras A, B y C?

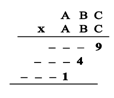17. En el alfamético que aparece a la derecha "9" representa la cifra 9 y cada una de las letras representa una cifra distinta de 9. Letras diferentes representan cifras diferentes. ¿Cuál es el número representado por "ONE"?

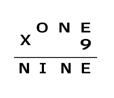18. Pablo eligió tres dígitos distintos y escribió todos los números de tres cifras que se forman con ellos (sin repeticiones). Luego sumó todos los números que obtuvo. Hallar la suma de Pablo, sabiendo que la suma de los dígitos originales es 14.

19. Hallar el menor número entero positivo tal que 5 veces el producto de sus cifras sea igual al número.

20. Sea A un conjunto de números naturales tal que:

1) Todos sus elementos son menores que 1000.

2) Ninguno de sus elementos es un cuadrado perfecto

3) El producto de dos cualesquiera de sus elementos es un cuadrado perfecto

¿Cuál es el mayor número de elementos que S puede tener?

21. En una urna se colocan 900 tarjetas del 100 al 999 y se mezclan perfectamente. Le pedimos a Julia que saque una tarjeta, anote la suma de los dígitos del número que sacó y rompa la tarjeta. ¿Cuál es el menor número de veces que debemos pedirle a Julia que repita esa operación para estar seguros de que anotará al menos tres veces la misma suma?

22. El boleto de entrada a un concierto a beneficio del Instituto Rioplatense de Promoción de la Matemática era un donativo de una cantidad entera menor que 500 pesos. Asistieron al concierto 1997 personas, entre argentinos, chilenos, uruguayos y brasileños.

a) Demuestra que hubo al menos dos personas de la misma nacionalidad que pagaron lo mismo.

b) Si el mayor número de veces que se repitió un donativo fue 10, se compraron boletos de cada uno de los precios y la cantidad recaudada fue la menor posible ¿cuántos boletos de cada uno de los precios se compraron?

Un número capicúa es aquel que se lee igual de izquierda a derecha que de derecha a izquierda, por ejemplo el número 4093904 es capicúa.

23. Con los dígitos a y b ( a desigual que 0, b desigual que 0) se forman los números:

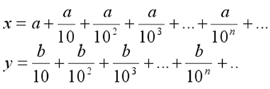Determinar todos los valores de los dígitos a y b que satisfacen que

es un número natural mayor o igual que 40.

24. Una máquina entrega 5 cobres por cada níquel que se le introduce y 5 níqueles por cada cobre que se le introduce. Decida si Pedro, que comienza con un solo cobre, puede, utilizando varias veces la máquina, finalizar con igual número de cobres que de níqueles.