Conteo
1. Si viaja en avión tiene 2 opciones, si viaja en camión tiene dos opciones, si viaja en tren tiene 2 opciones. En total tiene 2 × 3 = 6 opciones.
3. A la primera ciudad puede ir de seis maneras. Por cada una que escoja,
para llegar a la segunda ciudad tiene otras 6. Por lo tanto para llegar a la segunda
ciudad tiene 6×6=36 opciones.
En total lo puede hacer de 6 × 6 × 6 × 6 × 6 = 6 5 = 1296 formas.
3. La primera mujer puede escoger su pareja de baile de 10 maneras distintas. La segunda mujer, por cada elección de la primera mujer puede escoger a su pareja de 9 maneras distintas, o sea 10 × 9 = 90 combinaciones posibles. La tercera mujer podrá elegir de 8 maneras distintas a su pareja y así hasta la octava mujer que solo puede escoger de 3 formas distintas a su pareja. En total se pueden formar 10×9×8×7×6×5×4×3 = 1814400 parejas.
4. El primer múltiplo de tres es 12 y el último es 225. El número de múltiplos de 3 es entonces (225 - 12) ÷ 3 + 1= 72.
5. 48 = 2×2×2×2×3 Podemos formar los números usando estos dígitos o productos de estos dígitos que sean menores de 10 (y por lo tanto sigan siendo de 1 dígito). Los números serían todos los formados por los siguientes conjuntos de dígitos.
{2,2,2,2,3} {4,2,2,3} {4,4,3} {6,2,2,2} {8,2,3} {8,6}
Analizando los números diferentes que podemos formar en cada caso:
- 22223 el 3 puede estar en todas las posiciones ----- 5 números distintos
- 4223 para el primer dígito tenemos 3 posibilidades, para el segundo 2, para el tercero 2, para el cuarto 1 ----- 3×2×2 = 12 números distintos
- 443 el 3 puede estar en todas las posiciones ----- 3 números distintos
- 6222 el 6 puede estar en todas las posiciones ----- 4 números distintos
- 823 para el primero tenemos 3 posibilidades, para el segundo 2 y para el tercero 1 en total tenemos 3×2 = 6
- 86 para el primero tenemos dos posibilidades, para el segundo 1 ----- 2×1=2
Habrá 5 + 12 + 3 + 4 + 6 + 2 = 32 números diferentes.
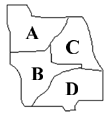
6. Como hay tres estados que se tocan tenemos que usar 3 o
4 colores.
|
 |
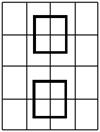
7. Primero vamos analizar solo la cuadricula de 4×4.
|
 |
8. Para que el número sea divisible entre 11, se necesita que la suma de los dígitos que ocupan una posición impar menos la suma de los dígitos que ocupan una posición par sea múltiplo de 11. En este caso la suma total de dígitos es 9×4 + 1×4 = 40, y podemos acomodarlos de forma que las sumas nos den: (en los productos el segundo número es 9 o 1 y el primero el número de veces que usamos cada uno).
| 4×9 - 1×4 = 32 no es múltiplo de 11. |
| 3×9 + 1×1 - (1×9 + 3×1) = 16 no es múltiplo de 11. |
| 2×9 + 2×1 - (2×9 + 2×1) = 0 si es múltiplo de 11. |
Necesitamos dos unos y dos nueves en las posiciones pares y lo
mismo en las posiciones impares. Las combinaciones que podemos hacer con dos unos y dos
nueves son:
| 1,1,9,9 | 1,9,1,9 | 1,9,9,1 |
| 9,9,1,1 | 9,1,9,1 | 9,1,1,9 |
Por cada una de estas seis combinaciones que tenemos en las posiciones pares tendremos
seis combinaciones posibles en las posiciones impares, por lo que en total serán 6×6 =
36 combinaciones.
9. 30 = 2×3×5. Formamos los números usando los dígitos y exploramos todas las posibilidades que hay con esos dígitos.
- 56 ----- 2
- 156 ----- 3×2×1 = 6
- 1156 ----- 3×2×2×1 = 12
- 11156 ----- 1×1×3×2×1 = 6 (el 1º y 2º dígito sólo tienen una posibilidad pues el número debe ser menor que 13000).
- 235 ----- 3×2×1 = 6
- 1235 ----- 4×3×2×1 = 24
- 11235 ----- 1×2×3×2×1 = 12 .
Hay 2 + 6 + 12 + 6 + 6 + 24 + 12 = 68 números.
| 10. El mínimo número de calles será cuando las calles no son concurrentes, pues en el cruce da cada dos calles habrá un farol. |
Analizando los dibujos podemos hacer la siguiente tabla:
Número de calles |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Número de faroles |
1 |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
45 |
55 |
66 |
El pueblo tiene 12 calles como mínimo. ¿Cómo podemos resolver el problema, sin tener que hacer una tabla, en el caso de tener un número mucho mayor de faroles? ¿Observas algún patrón de crecimiento en la tabla?
11. Podemos dividir los números del 1 al 15 en tres conjuntos según el residuo que dejan al dividirlos entre 3: A !’ los que dejan residuo 0, B ----- los que dejan residuo 1 y C ----- los que dejan residuo 2.
A = {3, 6, 9, 12, 15}, B = {1, 4, 7, 10, 13} y C = {2, 5, 8, 11, 14}
Tenemos que escoger tres números de forma que su suma sea divisible entre tres, esto
lo podemos hacer de varias formas:
- Sí el primer número lo escogemos del conjunto A y el segundo también, entonces el tercero tiene que ser necesariamente del conjunto A, para que al sumarlos el resultado sea divisible entre tres. Entonces los tres números son del conjunto A. Esto lo podemos hacer de 10 formas, ya que los números deben de ser diferentes.
- Ahora, sí el primer número es del conjunto A y el segundo es del B, entonces el tercero debe de ser del conjunto C. Podemos escoger 5 números del conjunto A, por cada uno 5 del B y por cada uno 5 del C, por lo que tenemos 5×5×5 = 125 formas de escogerlos.
- Sí el primer número es del A y el segundo del C, entonces el tercero es del B y ya lo contamos en el caso anterior.
Como no importa el orden de los números y ya vimos todas las opciones
cuando uno de ellos es del conjunto A, ahora tenemos que ver que pasa si no podemos tomar
elementos del conjunto A.
- Sí el primer número es de conjunto B y el segundo también, entonces necesariamente el tercero también es del conjunto B, y ya habíamos visto que podemos 10 formas de toma los tres números del mismo conjunto.
- Sí el primer número es del conjunto B y el segundo del C, entonces el tercero es del A y ya lo habíamos contado.
- Entonces ya solo nos quedan los casos el que los tres números son del conjunto C, que cuando los sumamos su resultado sí es divisible entre tres y estos los podemos tomar de 10 formas.
Entonces en total hay 10 + 125 + 10 + 10 = 155 formas de tomar tres números del 1 al 15 que su suma sea divisible entre tres.
14. Al pintar el cubo, todos los cubos externos quedan con alguna cara pintada. Si
quitamos las caras pintadas quedará un cubo de 8×8×8. Entonces las caras con al menos
una cara pintada serán: 10×10×10 - 8×8×8 = 488. Los cubos con una sola cara pintada
estarán en las caras del cubo de lado 10 formando cuadrados de 8×8,
como son 6 caras ----- serán 8×8×6 = 384 con una cara pintada. Entonces los cubos con
al menos dos caras pintadas serán: 488 - 384 = 104 (¿Qué pasa si el cubo es de 5×5×5
o de 15×15×15?).
13. Si el mensaje *§§**§* está formado por siete símbolos tendríamos una palabra.
Si tuviera un símbolo doble tendríamos 6 palabras según que el símbolo doble fuera
(*§), (§§), (§*), (**), (*§) ó (§*).
Si la palabra está formada por dos símbolos dobles tendríamos las siguientes posibilidades:
| (*§)(§*)*§* | (*§)§(**)§* | (*§)§*(*§)* | (*§)§**(§*) |
| *(§§)(**)§* | *(§§)*(*§)* | *(§)**(§*) | |
| *§(§*)(*§)* | *§(§*)*(§*) | ||
| *§§(**)(§*) |
Si la palabra está formada por tres símbolos dobles tenemos:
| (*§)(§*)(*§)* | (*§)(§*)*(§*) | (*§)§(**)(§*) |
*(§§)(**)(§*) |
En total tenemos 1 + 6 + 10 + 4 = 21 palabras posibles.
| 14. Como las rectas son concurrentes cada recta que se traza divide el plano en el
doble de regiones. En este caso como son 43 rectas, serán 43×2=86 regiones Al trazar una
recta no concurrente y no paralela podemos ver que, cuando tenemos: 2 rectas -----
aumenta 3 regiones El número de regiones que aumenta la recta es una más que el número de rectas concurrentes. En este caso serán 43+1=44 y con las regiones que ya teníamos 86+44=130 regiones |
|
15.
a) Podemos hacer una tabla
Marcela |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
Mirena |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
2 |
3 |
4 |
5 |
6 |
Juliana |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
6 |
5 |
4 |
3 |
2 |
1 |
Siguiendo con la tabla vemos que habrá 8 formas en que a Marcela le toque 1 balón, 7 formas de que le toquen 2, 6 formas de que le toquen 3, 5 formas de que le toquen 4, etc. Por lo tanto habrá: 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36 formas diferentes
| b) Análogamente con 100 balones tendríamos 98 formas de que le toque 1, etc. |
16.
a) En la fila 7 se pintan las casillas correspondientes a las columnas que son múltiplos de 7 y son en total |
|
b) En cada fila se pintan las casillas de las columnas que son múltiplos de las filas, por lo que en la fila 1 se pintan 100, en la 2 se pintan 100/2=50, etc. Podemos hacer una tabla:
# de fila |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
# de Casillas pintadas |
100 |
50 |
33 |
25 |
20 |
16 |
14 |
12 |
11 |
10 |
9 |
8 |
Total |
100 |
50 |
33 |
25 |
20 |
16 |
14 |
12 |
11 |
10 |
9 |
8 |
# de fila |
13-14 |
15-16 |
17-20 |
21-25 |
26-33 |
34-49 |
50 |
# de Casillas pintadas |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
Total |
14 |
12 |
20 |
20 |
24 |
32 |
1 |
La suma total de las casillas pintadas es 100 + 50 + 33 + ...
+ 24 + 32 + 1 = 431.
17. Tenemos de la pulsera 00000 a la 99999, es decir 100,000 pulseras. Pero al contar así
estamos contando cinco veces la misma pulsera ya que, por ejemplo, los números:
1-4-2-6-3, 3-1-4-2-6, 6-3-1-4-2, 2-6-3-1-4 y 4-2-6-3-1
representan la misma pulsera. Por lo tanto tenemos sólo 100,000/5 = 20,000 pulseras.
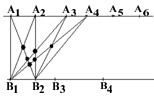
18. Los puntos de intersección se obtienen al intersectar las diagonales de los trapecios que se forman con dos puntos de la recta superior y dos puntos de la recta inferior, así que habrá tantos puntos de intersección como trapecios puedan formarse. En la figura aparecen los trapecios que se forman tomando los puntos B 1 y B 2 de la línea inferior y las combinaciones de dos puntos tomados de A 1, A 2, A 3 y A 4:, que son 6. El número total de trapecios que pueden formarse lo calculamos de la siguiente manera: De los puntos A 1, A 2, A 3 y A 4 A 5,
A 6 pueden tomarse parejas de 15 maneras distintas: el primer elemento de la
pareja lo podemos formar de 6 maneras y el segundo de 5 así que son 6×5 = 30, pero como
el orden no importa (la pareja A 1 - A 2, es la misma que, A 2
- A 1) tenemos la mitad de parejas, es decir 15. De los puntos B 1 y B 2 B 3 y B 4 podemos formar 4×3/2 = 6 parejas Así que, en total, podemos formar 15×6 = 90 trapecios y por lo tanto tendremos igual número de puntos de intersección. |
 |
Hay dos formas de construir el número de manera que la suma de sus dígitos sea par: a) tres dígitos pares ó b) un dígito par y dos impares.
a) Los pares considerados en el problema son {2, 4, 6, 8}. Para elegir el primer dígito tenemos 4 posibilidades, 3 para elegir el segundo y 2 para el tercer, en total, 4×3×2 = 24 posibilidades.
b) Los impares son {1, 3, 5, 7, 9}. Para elegir el número par tenemos 4 posibilidades y este puede ocupar tres posiciones distintas, en total 12 posibilidades. El primero de los dígitos impares podemos elegirlo de 5 maneras distintas y el segundo de 4 así que en total son 20 formas. Por lo tanto en este caso tenemos 20×12 = 240 posibilidades
La respuesta al problema es 24 + 240 = 264.
20.
a) Vamos a numerar los vértice del 1 al 8. Consideramos que el vértice donde se unen los dos lados iguales es el 1, entonces los triángulos isósceles que podemos formar son: 8,1,2; 7,1,3; 6,1,4. Tenemos 3 triángulos isósceles en cada vértice, entonces habrá 3x8=24 triángulos isósceles.
b) Existen 5 formas de pintar 3 vértices rojos y 5 azules: 3 rojos-5 azules, 2 rojos-4 azules-1 rojo-1 azul, 2 rojos-3 azules-1 rojo-2 azules, 1 rojo-1 azul-1 rojo-1 azul-1 rojo-3 azul, 1 rojo-1 azul-1 rojo-2 azul- 1 rojo-2 azul.
Vértices del mismo color:
3 r-5 a (1,2,3 r-4,5,6,7,8 a) |
1,2,3 | 4,5,6 | 5,6,7 | 6,7,8 | 4,6,8 |
2r-4a-1r-1 a (1,2,7r-3,4,5,6,8 a) |
3,4,5 | 4,5,6 | 4,6,8 | 3,6,8 | 3,5,8 |
2r-3a-1r-2 a (1,2,6r-3,4,5,7,8 a) |
3,4,5 | 3,5,7 | 3,5,8 | ||
1r-1a-1r-1a-1r-3 a (1,3,5r-2,4,6,7,8 a) |
1,3,5 | 2,4,8 | 2,4,6 | 4,6,8 | 6,7,8 |
1r-1a-1r-2a-1r-2 a (1,3,6r-2,4,5,7,8 a) |
1,3,6 | 2,4,8 | 2,5,7 | 2,4,7 | 2,5,8 |
Tenemos 5 + 5 + 3 + 5 + 5 = 23
21.
| a) Para ir de A a B es necesario moverse 6 casillas a la derecha y 4 arriba, en algún
orden. Si representamos los movimientos a la derecha y arriba con los símbolos !’ y !‘
respectivamente, una trayectoria de A a B equivale a una sucesión de 6 símbolos !’ y 4
símbolos !‘, en algún orden. El número de caminos posibles es: |
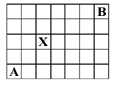 |
| b) Si debemos pasar por X, el número de caminos posibles será el producto del número de caminos de A a X y el número de caminos de X a B: | |
# de caminos de A a X: |
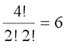 |
# de caminos de X a B: |
|
| # de caminos de A a B, pasando por X: | 15×6 = 90 |