Juegos y lógica
1. a) Cruzan los dos niños y uno se regresa con la lancha., b) cruza un soldado y el niño que se había quedado en esa orilla se regresa con la lancha; c) repetir a) y b) tantas veces como soldados haya.
2. a) el hombre cruza con el chivo y regresa, b) el hombre cruza con el costal de coles y se regresa junto con el chivo, c) el hombre cruza con el lobo y regresa por el chivo y cruza con él.
| 3. Como 10 no es divisible por 4, debe haber sillas que estén en las esquinas y cuenten en la suma de dos lados y como el residuo al dividir 10 por dos es 2, colocaremos dos sillas en las esquinas. De esta forma hay 3 sillas en cada pared. | 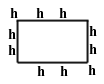 |
4. Para poder forzar la jugada ganadora, debemos decir el 27, así el otro jugador deberá
decir un número entre 27 y 31, inclusive. Para forzar decir nosotros el 27 antes debemos
decir el 22 y así sucesivamente.
La secuencia ganadora es 2---7---12---17---22---27. Si Juan comienza diciendo el 2, gana.
5. Puesto que 97 no es múltiplo de 3, la única forma de llegar a él es llegando a algún múltiplo de 3 mayor que él y luego oprimiendo la tecla B las veces que sea necesario. El múltiplo de 3 más cercano es 99. Para llegar al 99, la forma más eficiente es 11, 33 y 99. Para llegar al 11 llegamos antes al 12 y para esto necesitamos antes llegar al 3 así que la secuencia es:
Paso # |
Tecla |
Número |
Paso # |
Tecla |
Número |
|
0 |
1 |
6 |
A |
12 |
||
1 |
A |
3 |
7 |
B |
11 |
|
2 |
B |
2 |
8 |
A |
33 |
|
3 |
A |
6 |
9 |
A |
99 |
|
4 |
B |
5 |
10 |
B |
98 |
|
5 |
B |
4 |
11 |
B |
97 |
El número mínimo de veces que se deben oprimir las teclas es 11. Ya argumentamos que es necesario llegar a algún múltiplo de 3 mayor que 97, cualquier otro múltiplo de 3 que no sea 99 implicará, después de llegar a él, oprimir la tecla B 5 veces (si usamos el 102, para múltiplos mayores necesitaríamos 8 o más veces) para obtener el 97. Para llegar al 102 necesitamos la secuencia:
1---3---2---6---5---4---12---36---35---24---103
que requiere de oprimir 10 veces las teclas más otras 5 veces para llegar al 97.
6. Conviene agrupar los números por el residuo que dejan al ser divididos por 3: {1,4}, {2,5} y {3,6}. Para formar un número de tres dígitos que sea divisible por 3 es necesario escoger un dígito de cada uno de estos tres grupos y el jugador B no puede impedirlo. Si A escoge, por ejemplo el 1, B no tiene forma de que en sus siguientes turnos escoja un número entre {2,5} y otro entre {3,6}
7. La idea básica es formar tres grupos de monedas, dos de ellos con el mismo número y pesar estos dos últimos, si están equilibrados, entonces el tercer grupo contiene la moneda defectuosa, si no el platillo que pesa menos contiene la moneda defectuosa. En el peor de los casos tendríamos que hacer las siguientes pesadas (tomando los grupos con el mismo número de monedas y suponiendo que la moneda defectuosa está en uno de los grupos más grandes):
11,11,10 --- 4,4,3 --- 1,1,2 --- 1,1. En total 4 pesadas
En el caso general, es decir, si en lugar de 32 monedas,
tenemos n monedas entonces necesitaremos k pesadas si
3 k-1 < n < 3 k.
8. Empezamos con dos bolas x 1 y x 2 (x 1<x2) con lo cual eliminamos la bola x 2-x1. Al agregar una tercera bola x 3 eliminamos x 3-x1 pero podemos hacer que x 3-x2 = x 2-x1 para no eliminar otra más. Al agregar la bola x i tenemos que eliminar, necesariamente, la bola x i-x1. En el mejor de los casos si hemos echado n bolas debimos eliminar n-1 bolas. Por lo tanto, a lo más podremos tener 5 bolas en el saco. La solución es 5:
Bolas número: 1,3,5,7,9 ó 10,9,8,7,6
| 9. Una forma de acomodar las estrellitas es la siguiente: Si en el tablero hay menos de 7 estrellitas, entonces hay dos columnas que contienen ambas, a lo sumo dos de ellas. Se borran las otras dos columnas y dos filas que contengan las estrellitas restantes y así logramos borran todas. |
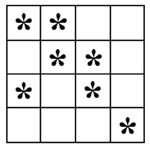 |
10. Cada jugada disminuye en uno el número de monedas sobre la mesa y aumenta en uno el número de columnas. Para alcanzar la situación final, el número de monedas sobre la mesa deberá ser múltiplo de 3. Supongamos que es posible lograr esa situación después de n jugadas, entonces el número de columnas será n + 1 y:
3(n + 1) = 1000 - n --- 4 n = 997, pero como 997 no es múltiplo de 4 el problema no tiene solución.
11. Una forma de lograrlo es la siguiente:
Jarra 1(6 lt.) |
Jarra 1(3.5 lt.) |
Jarra 1(2.5 lt.) |
6 |
0 |
0 |
2.5 |
3.5 |
0 |
2.5 |
1 |
2.5 |
5 |
1 |
0 |
5 |
0 |
1 |
1.5 |
3.5 |
1 |
1.5 |
2 |
2.5 |
4 |
2 |
0 |
4 |
0 |
2 |
0.5 |
3.5 |
2 |
0.5 |
3 |
2.5 |
3 |
3 |
0 |
12. Si en 5 partidos A y B tienen 3 aciertos cada uno, deben tener al menos un acierto común. El único pronóstico en el que coinciden es el partido 4 así el resultado de este partido fue empate (E) En los 4 partidos restantes A y B no comparten pronósticos y tienen 2 aciertos cada uno, son 4 en total. C no acertó el pronóstico del partido 4 y en los partidos 3 y 5 no comparte pronóstico con nadie así que los aciertos están en los partidos 1 y 2. B falló en el pronóstico de los partidos 1 y 2 así que debió acertar, además del partido 4 los partidos 3 y 5.Por lo tanto la boleta ganadora es la siguiente:
L |
E |
V |
|
1 |
X |
|
|
2 |
X |
|
|
3 |
X |
|
|
4 |
|
X |
|
5 |
X |
|
|
13. De i) podemos concluir que Z no ganó ya que como una de las dos proposiciones es
falsa entonces ganó X
o ganó Y.
a) Supongamos que ganó X. Entonces en ii) "Y llegó último" es falsa por lo que el orden de llegada es 1º X, 2º Y y 3º Z que es compatible con iii)
b) Supongamos que ganó Y. Entonces en ii) "X llegó antes que Z" es verdadera y el orden sería 1º Y, 2º X y 3º Z que también es compatible con iii).
Por lo tanto no podemos saber, con esta información en que orden llegaron los participantes.
| 14. El rectángulo que se forme tendrá 1056 de área. 1056 = 2 5×3×11. Puesto que uno de los cuadrados tiene 18 de lado, las posibles dimensiones de la nueva pieza son: 32×33, 24×22 o 22×48. La nueva pieza, de 32×33, se forma de la siguiente manera: Las cuatro esquina están formadas por los cuadrados de lado 18, 15, 14 y 9, siendo 15 y 9 esquinas opuestas. El cuadrado de 10 se coloca entre el de 14 y el de 9, mientras que el de 8 está entre el de 9 y el de 15 y 1, 4 y 7 están en el centro. |  |
| 15. El rectángulo de 3×8 se forma de la siguiente manera: El rectángulo de 5×10 no es posible formarlo porque su tiene área 50 que no es múltiplo de 4 que es el área de las piezas. |
|
16. Si sumamos los apretones de mano que dieron todas las personas, el número que obtenemos es par ya que cada apretón de manos lo estamos contando dos veces. Puesto que el número de apretones que suman aquellos que dieron un número par de apretones es par, la suma de apretones de quienes dieron un número impar de apretones también debe ser par lo que implica que el número de personas que dio un número impar de apretones es par.
17. Coloquemos en una rueda a las nueve personas a las que preguntó Juan y representémoslas con el número de apretones de mano que dio cada una.
En la rueda hay 9 personas, por lo que la persona que dio 8 apretones de mano sólo pudo saludar a siete de los que están la rueda (ya que no se puede saludar él mismo ni a su esposa) por lo que debió haber saludado a Juan y es pareja de quien no saludó a nadie. Siguiendo el mismo razonamiento encontramos que 7 también saludó a Juan y es pareja de 1, 6 también saludó a Juan y es pareja de 2, 5 saludó a Juan y es pareja de 3 y por lo tanto Juan es el esposo de 4, es decir, la esposa de Juan dio 4 apretones de mano.
18. La primera vez que se recorre la circunferencia tachando números se eliminan todos
los números pares. Si n es impar entonces el número que está a la izquierda del
1 es n que es impar, entonces después de tachar el último par, saltamos n
y tachamos el 1, entonces n debe ser par.
Pero si en después de completar una ronda, la cantidad de números que queda es impar,
caemos en el caso anterior y tacharemos el 1, por lo tanto n debe ser potencia de
2: n = 2 k.
19. En la cerrera de 50 m, Gerardo recorre solo 46 m, por lo que si la carrera fuera de 1000m, Gerardo recorrería (46/50)×1000 = 920 m.
Gerardo recorre 200 m en el mismo tiempo que Marcelo recorre 185 m, por lo que en el
tiempo en que Gerardo recorre 920 m, Marcelo recorrerá (185/200)×920 = 851 m.
Así pues, en el tiempo que Daniel corre 1000 m, Marcelo corre 851 m. Para llegar juntos a
la meta, Daniel debe darle a Marcelo 1000 - 851 = 149 m de ventaja.