Juegos y Lógica

1. Un destacamento de soldados debe cruzar un río. Ven una lancha con dos niños. La lancha es tan pequeña que sólo caben dos niños o un soldado. ¿Cómo deben hacer para cruzar todos los soldados?

2. Un hombre tiene que llevar a un lobo, un chivo y un costal de coles al otro lado del río. El bote tiene espacio para el hombre y el lobo o el chivo o el costal de coles. Si se lleva con él al costal de coles, entonces el lobo se come al chivo. Si se lleva al lobo, entonces el chivo se come las coles. Sólo cuando el hombre está presente, las coles y el chivo están a salvo de sus enemigos. ¿Cómo debe hacer el hombre para cruzar animales y coles del otro lado del río?

3. En un cuarto rectangular, ¿cómo se pueden colocar 10 sillas pegadas a la pared, de forma que el número de sillas en cada pared sea igual?

4. Juan y José juegan el siguiente juego: Juan dice un número entre 1 y 4. A continuación José le suma un número entre 1 y 4, al número resultante Juan le suma un número entre 1 y 4 y así sucesivamente. Gana el que llega al número 32. Encuentra, si es posible, una estrategia ganadora para Juan.

5. Inicialmente hay un 1 en la pantalla de una calculadora. Al apretar la tecla A, se multiplica por 3 el número de la pantalla. Al apretar la tecla B se resta 1 al número de la pantalla. Utilizando una secuencia de teclas A y B, hay que llegar a tener 97 en la pantalla. ¿Cuál es el número mínimo de veces que se deben oprimir en total las teclas?

6. A y B se alternan seleccionando un dígito entre los números 1,2,3,4,5,6 hasta que forman un número de 3 cifras. A gana si el número formado es divisible por 3 y si no lo es, pierde ¿Cuál es la estrategia ganadora de A al empezar?

7. Tenemos 32 monedas de aspecto idéntico pero una de ellas pesa menos que las demás. Tenemos también una balanza de platillos ¿Cómo podemos averiguar cuál es la moneda más ligera con sólo 4 pesadas? ¿Cuántas pesadas se necesitarían si tuviésemos n monedas en lugar de 32?

8. Se tienen bolas de billar numeradas del 1 al 10. Queremos echar en un saco la mayor cantidad posible de estas bolas con la siguiente condición: si una pareja de bolas está en el saco, no puede estar la bola numerada con su diferencia. Por ejemplo, si están la 3 y la 7, no puede estar la 4.
¿Cuál es el mayor número de bolas que podemos tener en el saco?

9. Demuestra que en un tablero de 4×4 es posible poner siete estrellitas de manera tal que si se borran dos filas y dos columnas cualesquiera del tablero, queda al menos una estrellita. Demuestra que si hay menos de siete estrellitas, siempre es posible borrar dos filas y dos columnas de manera tal que todas las casillas queden vacías.

10. En una mesa hay un cierto número de columnas de discos. Una jugada consiste en elegir una de las columnas, deshacernos de un disco y dividir lo que resta de la columna en dos columnas, no necesariamente iguales. Inicialmente hay sobre la mesa una sola columna que tiene 1000 discos. ¿Es posible, después de alguna sucesión de jugadas, llegar a una situación donde cada columna tenga exactamente 3 discos?

11. Tenemos una jarra con 6 litros de vino. Además tenemos dos jarras vacías con capacidades de 3.5 litros y 2.5 litros. Haciendo uso únicamente de las tres jarras, ¿cómo podemos obtener en las dos jarras de mayor capacidad tres litros de vino en cada una?

12. Tres apostadores A, B y C pronostican el resultado de cinco partidos de fútbol. (L = local, E = empate, V = visitante). Las boletas presentadas fueron:

L

E

V

L

E

V

L

E

V

1

X

1

X

1

X

2

X

2

X

2

X

3

X

3

X

3

X

4

X

4

X

4

X

5

X

5

X

5

X

Jugador A

Jugador B

Jugador C

¿Cuáles fueron los resultados de los cinco partidos?

13. Tres diarios cubren la información de una carrera de sólo 3 participantes: X, Y, Z. Extraemos dos afirmaciones de cada uno de ellos, una falsa y otra verdadera.

¿Es posible asegurar el orden en que llegaron los participantes? Justificar.

14. Las piezas de un rompecabezas rectangular son 9 cuadrados de lados 1, 4, 7, 8, 9, 10, 14, 15 y 18. ¿Cómo deben ubicarse las 9 piezas para armar el rompecabezas?

15. Se tiene una gran cantidad de piezas iguales, constituidas por cuatro cuadrados iguales de lado 1, con la siguiente forma Utilizando algunas piezas, ¿es posible formar un rectángulo cuyos lados midan 3 y 8, sin superponer las piezas ni dejar huecos? Utilizando algunas de estas piezas, ¿es posible formar un rectángulo cuyos lados midan 5 y 10, sin superponer las piezas ni dejar huecos? En los casos anteriores, si las respuesta es sí, indica cómo hacerlo. Si la respuesta es no, explique por qué.

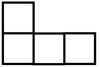16. Demuestra que el número de personas que ha dado un número impar de apretones de mano en una reunión, es par.

17. Cinco matrimonios van a una reunión. Por curiosidad Juan pregunta a cada uno de los demás asistentes cuántos apretones de mano dio. Obtiene las 9 respuestas posibles: 0, 1, 2, 3, 4, 5, 6, 7, 8,. ¿Cuál fue la respuesta de la esposa de Juan?

18. Escribimos los números 1, 2, 3 y 4 en una circunferencia. Empezando en el uno, tachamos cada segundo número hasta que quede sólo un número: primero tacho el 2, luego el 4 y por último el 3 quedando el 1 al final. Supongamos que escribo los números 1, 2, 3, ..., n en una circunferencia.
¿Para qué valores de n el último número que queda será el 1?

19. En una carrera de 50 m, Daniel le da 4 m de ventaja a Gerardo y llegan juntos a la meta. En una carrera de 200 m, si Gerardo le da 15 m de ventaja a Marcelo, llegan juntos a la meta. Suponiendo que corren a velocidad constante, ¿cuántos metros de ventaja deberá darle Daniel a Marcelo para llegar juntos a la meta en una carrera de 1000 m?

---