Problemas de ejemplo

La serie de problemas que presentamos a continuación nos permitirán ilustrar algunas de las estrategias básicas de la resolución de problemas.

Cotorra

C-1 Tenemos 10 focos. Al tocar uno de ellos todos cambian, el foco prendido se apaga y el foco apagado se prende, excepto el foco que se toca, que permanece como estaba . Se empieza con todos los focos prendidos. Explica que tienes que hacer para lograr que se apaguen todos los focos.

C-2 Una bolsa está llena con 71 dulces de los siguientes sabores: limón, naranja, uva y fresa. Hay el doble de dulces de limón que de fresa. Los dulces de naranja son uno menos que los de fresa. Hay seis dulces menos de uva que de limón.

a) ¿Cuál es el mínimo número de dulces que tienes que sacar para estar seguros de tener por lo menos dos dulces del mismo sabor?

b) ¿Cuál es el número mínimo de dulces que tienes que sacar para tener dulces de por lo menos dos sabores?

C-3 Eder y Elena juegan al juego del 100. Se empieza diciendo el número 3. En cada jugada se debe decir un número mayor que el último que se haya dicho pero menor que su doble. Gana quien diga el 100. Encuentra una estrategia ganadora.

Nivel I

I-1 Se escriben 3000 dígitos, uno después del otro, de modo que todo par de dígitos consecutivos forme un número de dos cifras que sea el producto de cuatro primos (no necesariamente distintos), es decir, que el primer y segundo dígitos formen un número de dos cifras que sea el producto de cuatro primos, el segundo y tercer dígitos formen un número de dos cifras que sea el producto de cuatro primos y así sucesivamente. ¿Qué dígito ocupa la posición 1999? Nota: El número 1 no es primo.

I-2 En una circunferencia se marcan los puntos A, B, C, D, E y F a igual distancia entre sí. Se dibujan polígonos convexos que tienen sus vértices en algunos o en todos los puntos marcados. ¿Cuántos polígonos distintos se pueden dibujar? ¿Cuántos de esos polígonos son regulares?

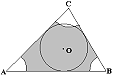
I-3 La circunferencia de centro O tiene 5 cm de radio. El triángulo ABC tiene 84 cm de perímetro y sus lados son tangentes a la circunferencia de centro O. Los arcos de circunferencia con centro en cada vértice del triángulo tienen 4 cm de radio. ¿Cuál es el área de la zona sombreada?


Nivel II

II-1 Aline, Mirena e Isabel escriben números naturales de cuatro cifras diferentes formados por los dígitos 1, 2, 3 y 4.
  • Aline hace una lista de todos los que tienen la primera cifra igual a 1.
  • Mirena hace la lista de todos los que tienen las dos primeras cifras formadas por los dígitos 1 y 2 en cualquier orden.
  • Isabel hace la lista de todos los que tienen las tres primeras cifras formadas por los dígitos 1, 2 y 3 en cualquier orden.
    ¿Cuántos son los números naturales de cuatro cifras que no aparecen en ninguna de las listas?
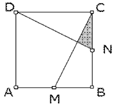
II-2 Sea ABCD un cuadrado con lado 1 cm. Si M y N son los puntos medios de los lados AB y BC, respectivamente, ¿cuál es el área de la zona sombrada?

II-3 En un tablero de 10×10 se escribe un número en cada casilla de modo tal que la diferencia entre los números colocados en casillas adyacentes sea siempre menor o igual que 1 (dos casillas son adyacentes si tienen un lado común).
  • Muestre un tablero que tenga la mayor cantidad posible de números distintos, y explique por qué no puede haber un tablero que tenga más números distintos.
  • Demuestre que en el tablero hay al menos un número que se repite 6 veces o más.


Soluciones

Cotorra

C-1 Tenemos 10 focos. Al tocar uno de ellos todos cambian, el foco prendido se apaga y el foco apagado se prende, excepto el foco que se toca, que permanece como estaba . Se empieza con todos los focos prendidos. Explica que tienes que hacer para lograr que se apaguen todos los focos.

Con el fin de entender bien las reglas del problema y tratar de ir encontrando algún patrón de comportamiento que nos ayude a hallar la solución es recomendable comenzar a tocar focos y ver que ocurre. Para ello es conveniente idear una forma eficiente de representar la hilera de los 10 focos en cada momento. En este caso nos será útil elaborar una tabla: usaremos X para focos prendidos y O para focos apagados. Empezamos con los 10 focos prendidos

Paso #
F1
F2
F3
F4
F5
F6
F7
F8
F9
F10
0
X
X
X
X
X
X
X
X
X
X

Tocamos un foco, el primero por ejemplo, y obtenemos

Paso #
F1
F2
F3
F4
F5
F6
F7
F8
F9
F10
0
X
X
X
X
X
X
X
X
X
X
1
X
O
O
O
O
O
O
O
O
O

Toquemos otro foco, diferente del primero, porque si no, regresaríamos a la configuración inicial: toquemos el segundo foco.

Paso #
F1
F2
F3
F4
F5
F6
F7
F8
F9
F10
0
X
X
X
X
X
X
X
X
X
X
1
X
O
O
O
O
O
O
O
O
O
2
O
O
X
X
X
X
X
X
X
X

Al comparar el estado de focos con la situación original vemos que después de tocar dos focos, aquellos que no fueron tocados quedan como estaban originalmente. Toquemos sucesivamente los focos 3 y 4 para obtener:

Paso #
F1
F2
F3
F4
F5
F6
F7
F8
F9
F10
0
X
X
X
X
X
X
X
X
X
X
1
X
O
O
O
O
O
O
O
O
O
2
O
O
X
X
X
X
X
X
X
X
3
X
X
X
O
O
O
O
O
O
O
4
O
O
O
O
X
X
X
X
X
X

Continuamos tocando los focos sucesivamente y obtenemos:

Paso #
F1
F2
F3
F4
F5
F6
F7
F8
F9
F10
0
X
X
X
X
X
X
X
X
X
X
1
X
O
O
O
O
O
O
O
O
O
2
O
O
X
X
X
X
X
X
X
X
3
X
X
X
O
O
O
O
O
O
O
4
O
O
O
O
X
X
X
X
X
X
5
X
X
X
X
X
O
O
O
O
O
6
O
O
O
O
O
O
X
X
X
X
7
X
X
X
X
X
X
X
O
O
O
8
O
O
O
O
O
O
O
O
X
X
9
X
X
X
X
X
X
X
X
X
O
10
O
O
O
O
O
O
O
O
O
O

La solución consiste en tocar los focos de manera sucesiva y al final todos estarán apagados.
En este problema la solución fue surgiendo prácticamente sola. Lo importante fue tener una forma eficiente de representar los focos y sus cambios. ¿Qué ocurre si modificamos ligeramente las condiciones del problema? Por ejemplo, si en lugar de tener 10 focos tuviéramos 4, 8 o 2000, ¿el método para apagarlos todos seguiría funcionando? ¿Y si fueran 3 o 1999 también funcionaría? Dejaremos que el lector responda la primera pregunta y nosotros analizaremos la segunda.
Veamos primero que ocurre con 3 focos. Toquémoslos de manera sucesiva como cuando teníamos 10.

Paso #
F1
F2
F3
0
X
X
X
1
X
O
O
2
O
O
X
3
X
X
X

Nuestro método no sirve: nos regresa al estado original. ¿Podemos encontrar otro método para apagar los focos? Veamos: si empezamos con F1 (o cualquiera de los otros dos focos) en el segundo paso debemos cambiar de foco, digamos tocar F2. Ya vimos que tocar F3 no conduce a nada. Probemos tocar nuevamente F1:

Paso #
F1
F2
F3
0
X
X
X
1
X
O
O
2
O
O
X
3
O
X
O

No avanzamos: seguimos teniendo un foco prendido y dos focos apagados. Si elegimos uno de los focos apagados tendremos en el siguiente renglón nuevamente uno prendido y dos apagados pero si elegimos el foco prendido entonces acabamos con los tres focos prendidos, como al principio. Hemos examinado todas las posibilidades por lo que podemos estar seguros de que iniciando con tres focos prendidos nunca podremos llegar a tenerlos todos apagados.

Pero, ¿qué ocurre si tenemos 1999 focos? Evidentemente no podemos examinar todas las posibilidades; tendremos que buscar otro tipo de argumento.

Por lo que hemos visto hasta ahora, todo apunta a que cuando el número de focos es par se puede apagarlos simplemente eligiéndolos uno a la vez hasta terminar y pareciera que cuando el número de focos es impar resulta imposible apagarlos todos. ¿Podemos encontrar una razón para que esto sea así? En el caso de tres focos, notemos que el número de focos prendidos siempre es 1 o 3, es decir, un número impar.

Supongamos que tenemos un número impar de focos, de los cuales un número par de ellos está apagado y el resto (un número impar) está prendido:

Tenemos dos posibilidades, elegir un foco prendido o uno apagado:

1. Elegimos un foco prendido, digamos el último de ellos (en realidad da igual cual de los prendidos elijamos). Tendremos que todos los prendidos menos uno se apagan y como era impar el número de prendidos y apagamos todos menos uno, tendremos que el número de focos apagados es par. Todos los apagados se prenden, era un número par de apagados, más el foco elegido que permanece prendido, resulta que tenemos nuevamente un número impar de focos prendidos.

2. Elegimos un foco apagado, digamos el primero de ellos. Entonces todos los prendidos, que es un número impar, más el que elegimos estarán apagados y todos los que estaban apagados, que es un número par, menos el que elegimos, se encenderán, es decir, tendremos nuevamente un número impar de focos prendidos.


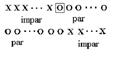Resumiendo. Iniciamos con número impar de focos prendidos y hemos visto que ya sea que elijamos un foco apagado o uno prendido, el número de focos prendido siempre será impar y puesto que 0 es par, nunca podremos tener 0 focos prendidos, o sea, todo los focos apagados.

C-2 Una bolsa está llena con 71 dulces de los siguientes sabores: limón, naranja, uva y fresa. Hay el doble de dulces de limón que de fresa. Los dulces de naranja son uno menos que los de fresa. Hay seis dulces menos de uva que de limón.


a) ¿Cuál es el mínimo número de dulces que tienes que sacar para estar seguros de tener por lo menos dos dulces del mismo sabor?

b) ¿Cuál es el número mínimo de dulces que tienes que sacar para tener dulces de por lo menos dos sabores?

1. Por supuesto que si tenemos suerte, con dos dulces que saquemos podríamos tener los dos del mismo sabor pero ¿y si la suerte no nos favorece, como podemos estar seguros de tener un sabor repetido? Lo peor que nos puede pasar es que al sacar 4 dulces los cuatro sean de distinto sabor pero sin duda el quinto dulce que saquemos tendrá uno de los sabores que ya tenemos. La respuesta a esta pregunta es 5.


2. Para responder esta pregunta debemos saber antes cuántos dulces hay de cada sabor. De las condiciones del problema se desprende que del sabor que más dulces hay es de limón. Además como los de limón son el doble de los de fresa, la cantidad de dulces de limón es par. Si dividimos los 71 dulces entre los 4 sabores obtenemos 17.75. Puesto que la cantidad de dulces de limón está claramente encima del promedio, comencemos con 20 de limón y hagamos una tabla para ir encontrando las cantidades de dulces de los otros sabores.


Limón
Fresa
Naranja
Uva
Total
20
10
9
14
53
22
11
10
16
59
24
12
11
18
65
26
13
12
20
71

Ya sabemos cuántos dulces hay de cada sabor. Lo peor que nos puede pasar es que los primeros 26 sean de limón, que es el sabor que más se repite, pero sin duda el dulce número 27 que saquemos tendrá otro sabor.

La idea utilizada para responder la pregunta del inciso a) es conocida como el Principio de Dirichlet.

 


C-3 Eder y Elena juegan al juego del 100. Se empieza diciendo el número 3. En cada jugada se debe decir un número mayor que el último que se haya dicho pero menor que su doble. Gana quien diga el 100. Encuentra una estrategia ganadora.

Hay muchos problemas que se pueden resolver mediante una estrategia que podemos llamar desandar lo andado . Vamos a suponer que ya llegamos a nuestra meta, es decir que ya encontramos la estrategia ganadora y por tanto dijimos el 100. Esto significa que obligamos a nuestro contrincante a decir un número mayor que la mitad de 100, que es 50 o sea que lo forzamos a decir un número mayor que 50 y menor que 100 y esto sólo es posible si nosotros dijimos antes el 50. Parte de la estrategia ganadora es decir el 50 así nuestro compañero de juego dirá un número entre 51 y 99, inclusive, y luego nosotros decimos el 100. ¿Qué tenemos que hace para poder decir el 50? Repetimos el análisis que hicimos antes y nos damos cuenta que debemos nosotros decir el 25 y para esto antes debemos decir el 12, antes el 6 y primero el 3. Por lo tanto quien empieza gana y la estrategia consiste en decir la secuencia 3-6-12-25-50-100.

Cambiemos las condiciones del problema y veamos si nuestro método sigue siendo eficaz. ¿Qué pasa si en lugar de que se gana al decir el 100 triunfa quien diga el 223? Aplicando el método de desandar lo andado encontramos la estrategia ganadora, en este caso la secuencia 3-6-13-27-55-111-223. Otra vez gana quien empieza. ¿Podría el lector cambiar el 223 por otro número de forma que ganase quien no empieza?
También podemos utilizar el mismo método en problemas con reglas diferentes, por ejemplo:
  1. Gana quien diga el 32. En cada jugada se le puede sumar 1, 2, 3 o 4 al número anterior.
  2. Gana quien diga el 1000. Se empieza con el 2. En cada jugada debe decirse un número mayor que el anterior pero menor que su cuadrado.

Nivel I

I - 1 Se escriben 3000 dígitos, uno después del otro, de modo que todo par de dígitos consecutivos forme un número de dos cifras que sea el producto de cuatro primos (no necesariamente distintos), es decir, que el primer y segundo dígitos formen un número de dos cifras que sea el producto de cuatro primos, el segundo y tercer dígitos formen un número de dos cifras que sea el producto de cuatro primos y así sucesivamente. ¿Qué dígito ocupa la posición 1999? Nota: El número 1 no es primo.

La primera pregunta que surge es ¿qué números de dos dígitos podemos formar con el producto de cuatro
números primos? Nos dicen que los cuatro primos no tienen que ser diferentes, así por ejemplo podemos formar el
16 = 2×2×2×2 o el 36 = 2×2×3×3. Un punto importante es encontrar una manera sistemática de generar todos los números que necesitamos. Una forma de hacerlo es la siguiente. Los números en cuestión tendrán cuatro doses, tres doses, dos doses, un dos o ningún dos. Estos cinco casos cubren todas las posibilidades.

1. Cuatro doses. Sólo está el 16=2×2×2×2

2. Tres doses.

2×2×2×3 = 24
2×2×2×5 = 40
2×2×2×7 = 56
2×2×2×11 = 88
2×2×2×13 = 104 no es un número de dos dígitos.

3. Dos doses.

2×2×3×3 = 36
2×2×3×5 = 60
2×2×3×7 = 84
2×2×5×5 = 100 no es un número de dos dígitos

4. Un dos.

2×3×3×3 = 54
2×3×3×5 = 90
2×3×3×7 = 126 no es un número de dos dígitos

5. Ningún dos.

3×3×3×3 = 81
3×3×3×5 = 135 no es un número de dos dígitos

Agrupémoslos de acuerdo con sus terminaciones:

40 60 90
24 54 84
16 36 56
81
88

Intentemos usar estos números, de acuerdo con las reglas, para formar un número de 3000 dígitos. Al leer el problema vemos que se debe cumplir que todo par de dígitos consecutivos forme un número de dos cifras... , esto significa que el dígito de las unidades del primer producto de primos será el dígito de las decenas del segundo producto y así sucesivamente. No podemos usar el 40 porque el número formado por los dígitos 2 y 3 no sería un número de dos dígitos puesto que empezaría con 0. Lo mismo ocurre con el 60 y el 90. Empecemos con el 24. El siguiente número tendría que ser 0 (240) pero ya no podemos seguir agregando números. Lo mismo ocurre con el 54 y el 84. Probemos el 16. Debería seguir un 0 (160) y ya no podemos continuar. Lo mismo ocurre con el 36 y el 56. El 81 no lo podemos usar puesto que el único de nuestros números que empieza con 1 es el 16 y tendríamos que usar después el 60 y ya no podríamos. Una manera de formar el número de 3000 dígitos es que todos los dígitos sean ochos. Otra posibilidad es que los últimos tres números sean 160 y todos los demás sean ochos. En ambos casos el número que ocupa la posición 1999 es un 8.

¿Qué ocurriría si en lugar de formar el número de 3000 dígitos con números de dos dígitos formados por cuatro primos pedimos que sean números de dos dígitos formados por 3 primos o por 5 primos?

I - 2 En una circunferencia se dibujan los puntos A, B, C, D, E y F a igual distancia entre sí.
Se dibujan polígonos convexos (aquel que tiene todos sus ángulos internos menores a 180º) que tienen sus vértices en algunos o en todos los puntos marcados. ¿Cuántos polígonos distintos se pueden dibujar? ¿Cuántos de esos polígonos son regulares?
Comencemos por hacer un esquema. Nuevamente, el problema consiste en diseñar una forma sistemática de ir contando los polígonos. Lo haremos según su número de lados, que pueden ser 6, 5, 4 o 3.


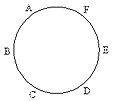1. Seis lados. Sólo hay uno, el hexágono regular usando los 6 vértices.

2. Cinco lados. Usamos cinco vértices, por lo que quitamos un vértice cada vez, es decir que serán 6. Todos son irregulares.

3. Cuatro lados. Usamos cuatro vértices, es decir que quitamos dos vértices cada vez. Fijémonos en los vértices que quitamos:

AB, AC, AD, AE, AF
  BC, BD, BE, BF
    CD, CE, CF
      DE, DF
        EF

Son en total 1 + 2 + 3 + 4 + 5 = 15, todos irregulares.

4. Tres lados. Usamos tres vértices. Es equivalente contar los vértices que usamos o los que quitamos y como son tres y tres, da igual contar unos u otros.

Con A

ABC ABD ABE ABF
  ACD ACE ACF
    ADE ADF
      AEF

Son en total 1 + 2 + 3 + 4 = 10 y sólo 1 regular (ACE)

Sin A

Con B

BCD BCE BCF
  BDE BDF
    BEF

Son en total 1 + 2 + 3 = 6 y sólo 1 regular (BDF)

Sin B

CDE CDF  
  CEF  
    DEF

Son en total 4 todos irregulares.

Tenemos en total 15 + 10 + 6 + 4 = 35 polígonos, de los cuales sólo 3 son regulares.

I-3 La circunferencia de centro O tiene 5 cm de radio. El triángulo ABC tiene 84 cm de perímetro y sus lados son tangentes a la circunferencia de centro O. Los arcos de circunferencia con centro en cada vértice del triángulo tienen 4 cm de radio. ¿Cuál es el área de la zona sombreada?


La parte sombreada no es una figura cuya área pueda ser obtenida por medio de una fórmula conocida. ¿Podemos encontrar el área a partir del área de figuras que sí conocemos y que están relacionadas con ella?

El área sombreada es igual al área del triángulo menos los sectores del círculo que están en cada vértice. ¿Podemos conocer estas dos áreas?

De los sectores circulares que están en cada vértice sabemos que provienen de una circunferencia de radio 4 cm. No sabemos cuanto mide cada ángulo del triángulo, por lo que no sabemos cuál es el área de cada uno de estos sectores circulares pero sí podemos saber cuanto suman sus áreas ya que la suma de los ángulos internos del triángulo es 180º así que la suma de sus áreas equivale al semicírculo de radio 4 cm, es decir, ½ pi×4 al cuadrado = 8pi.

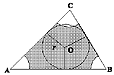Del triángulo sabemos que su perímetro es 84 cm y que tiene inscrita una circunferencia de radio 5. En el punto de tangencia el radio y el lado del triángulo son perpendiculares. Podemos pensar el triángulo original como formado por los triángulos AOB, BOC y COA. Entonces:

área ABC = área AOB + área BOC + área COA
= ½ (AB×r + BC×r + CA×r)
= ½ r (AB + BC + CA)
= 5/2(84) = 210

Por lo tanto el área de la figura sombreada es 210 - 8pi

Nivel II

II - 1 Aline, Mirena e Isabel escriben números naturales de cuatro cifras diferentes formados por los dígitos 1, 2, 3 y 4.
  • Aline hace una lista de todos los que tienen la primera cifra igual a 1.
  • Mirena hace la lista de todos los que tienen las dos primeras cifras formadas por los dígitos 1 y 2 en cualquier orden.
  • Isabel hace la lista de todos los que tienen las tres primeras cifras formadas por los dígitos 1, 2 y 3 en cualquier orden.
¿Cuántos son los números naturales de cuatro cifras que no aparecen en ninguna de las listas?

Utilicemos una forma sistemática de contar los números buscados. Examinemos cifra por cifra cuáles son las posibilidades. Una representación gráfica de los números en cada lista puede ayudar:

Aline: 1XXX

Mirena 12XX o 21XX

Isabel XXX4

De los números buscados:

1. La primera cifra no puede ser 1, porque estaría en la lista de Aline

2. La primera cifra es 2. Entonces la segunda cifra no puede ser 1, porque el número estaría en la lista de Mirena. El último número no puede ser 4 porque está en la lista de Isabel. Las posibilidades son:

    2341

    2431
    2413

3. La primera cifra es 3. La última cifra no puede ser 4 así que las posibilidades son:

3412
3421
3142
3241

4. Faltan los que empiezan con 4

4123
4132
4213
4231
4312
4321

En total son 13 números que no están en ninguna de las listas. Podríamos extender el problema y preguntar ¿Cuántos números están en las 3 listas? o ¿Cuántos están en al menos dos de las listas?

II - 2 Sea ABCD un cuadrado con lado 1 cm. Si M y N son los puntos medios de los lados AB y BC, respectivamente, ¿cuál es el área de la zona sombreada?

A diferencia del problema de geometría anterior, en este caso la figura cuya área debemos encontrar es un triángulo con fórmula conocida: la mitad de la base por la altura. Esto nos sugiere buscar estos valores. La base CN la conocemos, es ½ pero falta conocer la altura. La altura IR está determinada por la intersección de los segmentos DN y CM así que debemos utilizar sus características para determinarla.

Una forma de hacerlo es estableciendo semejanzas de triángulos: los triángulos CIR y CMB son semejantes, y también lo son los triángulos CMB y CNI. En efecto, los triángulos CIR y CMB son semejantes puesto que el ángulo MCB es común a ambos y los ángulos IRC y MBC son rectos. En el caso de los triángulos CMB y CNI comparten el ángulo MCB y " INC = " CMB ya que los triángulos DNC y MBC son congruentes (CD = CB, MB = CN y " C = " B) por lo que " INC es complementario de " NDC que es igual al " MCB, por lo tanto " INC = " CMB.

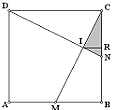Solución 1 (CIR = CMB) :

CR + RN = ½ .
CIR = CMB - IR/CR = MB/CB = ½ - CR = 2IR
IRN = DCN - RN/IR = CN/DC = ½ - RN = IR/2
IR/2 + 2IR = ½ !’ IR = 1/5. -

Área INC = ½ ( ½ × 1/5) = 1/20.

Solución 2 (CMB = CNI) :
Aplicando el teorema de Pitágoras obtenemos MC

MC =
= raíz de 5/2. MC/BC = raíz de 5 = NC/IC - IC = 1/raíz de 5 y IN = 1/2raíz de 5 -

Área INC = ½ ( 1/raíz de 5 × 1/2 raíz de 5) = 1/20.

Solución 3:

Trazamos PB paralelo a DN, QN paralelo a CM y OQ paralelo a CB. Se forman cuatro triángulos que son congruentes al triángulo sombreado y, puesto que los cinco forman el triángulo CMB, que es un ¼ del área del triángulo, entonces el área del triángulo sombreado es 1/20.(Por supuesto, en un concurso es necesario demostrar cada una de las congruencias de triángulos.)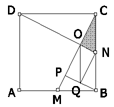

Podemos investigar muchos otros problemas que se derivan de éste:
  1. Supongamos que N divide al segmento BC en una razón dada.
  2. Supongamos que M divide al segmento AB en una razón dada.
  3. Supongamos que en lugar de cuadrado tenemos un rectángulo cuyos lados están en una razón dada.
  4. Supongamos que en lugar de cuadrado o rectángulo tenemos un paralelogramo.
II-3 En un tablero de 10×10 se escribe un número en cada casilla de modo tal que la diferencia entre los números colocados en casillas adyacentes sea siempre menor o igual que 1 (dos casillas son adyacentes si tienen un lado común).
  • Muestre un tablero que tenga la mayor cantidad posible de números distintos, y explique por qué no puede haber un tablero que tenga más números distintos.
  • Demuestre que en el tablero hay al menos un número que se repite 6 veces o más.
Puesto que la diferencia entre las casillas debe ser menor o igual que 1, comencemos poniendo la primera hilera del 1 al 10.

1
2
3
4
5
6
7
8
9
10

La primera casilla de la segunda fila puede ser 0, 1 o 2. Pero nos conviene poner el 2 porque así al final de la hilera tendremos el 11 que es un número que no hemos utilizado y se trata de tener la mayor cantidad de números distintos

1
2
3
4
5
6
7
8
9
10
2
3
4
5
6
7
8
9
10
11

Siguiendo esta misma idea completamos fácilmente el resto de la tabla.

1
2
3
4
5
6
7
8
9
10
2
3
4
5
6
7
8
9
10
11
3
4
5
6
7
8
9
10
11
12
4
5
6
7
8
9
10
11
12
13
5
6
7
8
9
10
11
12
13
14
6
7
8
9
10
11
12
13
14
15
7
8
9
10
11
12
13
14
15
16
8
9
10
11
12
13
14
15
16
17
9
10
11
12
13
14
15
16
17
18
10
11
12
13
14
15
16
17
18
19

Por supuesto que pudimos haber empezado con cualquier número en lugar del 1 y hubiésemos obtenido, siguiendo este método, un tablero que cumpliría las condiciones del problema. ¿Cómo podemos estar seguros de que no es posible construir otro tablero que tenga una mayor cantidad de números diferentes?

Si pensamos en recorrer el tablero viajando por casillas adyacentes y utilizando los caminos más cortos, la máxima distancia que podemos viajar es de esquina a esquina, cruzando 18 casillas, por lo tanto a partir de un número n sólo podríamos tener n + 18 en la otra esquina, es decir 19 números diferentes.

El segundo inciso del problema se resuelve con una sencilla aplicación del Principio de Dirichlet: si tenemos en total 10 × 10 = 100 números y a lo más hay 19 diferentes entonces podemos estar seguros de que al menos uno de los números se repetirá [(100 - 1)/19] + 1 veces, es decir, 6 veces.