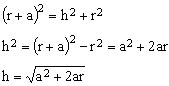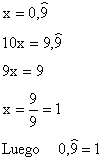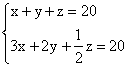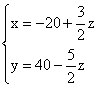Problemas de
Cosas interesantes
Material áulico
Alumnos
Cartelera
Material para
registrados
Tus otras materias
Contactarme
|
¿Es primo el número 333333331? Como estamos en el número 31 de Epsilones es un buen momento, otro lo será en el número 331, para plantear la siguiente cuestión. Los números 31, 331, 3331, 33331, 333331, 3333331, 33333331 son primos. ¿Lo es el 333333331? Fermat’s Last Theorem, pp.177-178. |
|
Una relación de equivalencia es aquella que cumple las propiedades reflexiva, simétrica y transitiva. Sin embargo... Sea R una relación que cumple las propiedades simétrica y transitiva. Por cumplir R la propiedad simétrica, dados a y b tales que aRb, entonces bRa. Como aRb y bRa y dado que R es transitiva, aRa. Es decir, R es reflexiva. Hemos demostrado que simetría + transitividad implican reflexividad, lo cual nos permite sacar la reflexividad de la definición de relación de equivalencia, ¿no? Fue Lorenzo el que me planteó la cuestión. |
|
El número de espectadores La capacidad de un estadio de fútbol es de 25000 espectadores. En un partido reciente el campo estaba prácticamente lleno. Un estadístico muy dado a los porcentajes comprobó que el 15,555…% de los espectadores estaban en el graderío sur y que el 24,524524… % de los espectadores eran mujeres. ¿Cuántos espectadores asistieron? Algoritmo, matemáticas 1. |
|
Las tres llaves de luz En el sótano hay tres llaves de luz y en el tercer piso están las bombillas que se encienden con esas cada una de esas llaves. El problema es que no se sabe cual llave corresponde a cada foco y la única manera de averiguarlo sería usando la llave y subir al tercer piso para comprobar. ¿Cuál es el procedimiento para subir la menor cantidad de veces al tercer piso y conocer que llave le corresponde a cada bombilla? Enviado por Eletema el 31-3-2005. |
|
Café: ¿solo o con leche? ¿Qué se enfría antes, una pequeña taza de café solo o una gran taza de café con leche? Aunque la pregunta me fue planteada más o menos así, para concretar y no liarnos con calores específicos y demás vamos a suponer dos tazas semejantes (es decir, con exactamente la misma forma pero de distinto tamaño) y con el mismo tipo de líquido en su interior: ¿cuál se enfría antes? ¿Por qué? |
||||||||||||||||||||||||||||||||
|
Veinte panes para veinte personas Veinte panes para veinte personas, los niños a medio pan, las mujeres a dos y los hombres a tres. ¿Cuántos hombres, niños y mujeres había? Tenti (4-3-2004) envía este problema popular de la campiña de Córdoba. |
||||||||||||||||||||||||||||||||
|
Los monjes lógicos En un perdido monasterio viven unos monjes de clausura, todos ellos especialistas en lógica, que tienen prohibido por su regla comunicarse entre sí por ningún medio. Tan sólo se reúnen una vez al día en el refectorio y se sientan a comer en una gran mesa redonda sin comunicarse de ninguna forma; ni hablando ni por señas ni escribiendo. Un día les visita el superior de la orden, que no tiene esta restricción y les dice en el refectorio: “Esta noche os ha visitado un ángel y a los elegidos os ha dibujado una marca en la frente. En cuanto sepáis quienes sois los elegidos, tras la comida partiréis inmediatamente a la ermita del monte a pasar una semana en oración.” No ocurre nada hasta el séptimo día, en el que los monjes restantes comprueban a la hora de la comida que faltan los compañeros elegidos.
Jesús M. Landart manda (18-9-2003) este sorprendente problema con dos posibles soluciones en las que los monjes, y esto es una pista, ni siquiera tienen que cambiar de sitio en la mesa. Nota: para evitar ambigüedades consideraremos que el primer día es el siguiente al de la visita del superior. |
||||||||||||||||||||||||||||||||
|
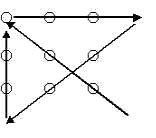
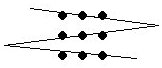
Nueve puntos Se trata de unir los nueve puntos que ves en la figura mediante cuatro segmentos dibujados sin levantar el lápiz del papel.
Yon (4-3-2003) manda este otro clásico, uno de los más citados por los psicólogos a propósito del tema de la autolimitación. |
||||||||||||||||||||||||||||||||
|
Alicia en el Bosque del Olvido Cuando Alicia entraba en el Bosque del Olvido, a menudo olvidaba su nombre y algunas veces hasta el día de la semana. No obstante, dos extraños animales, un león y un unicornio, asiduos del bosque, le daban alguna pista para averiguar el día en el que se encontraba.
Un día Alicia entró en el bosque y se encontró con los dos animales que le dijeron:
Alicia, que era muy inteligente, supo deducir a partir de estos comentarios qué día de la semana era. ¿Cuál era ese día? Juan Carlos Pérez (29-6-2003) manda este acertijo lógico con personajes de Alicia a través del espejo. |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
Tres sombreros Tres personas llevan un sombrero (blanco o negro) del que no conocen el color, aunque saben que todos no son blancos. Las tres personas están sentadas una detrás de otra, de modo que el último puede ver el color de los sombreros del primero y del segundo, mientras que el segundo puede ver el color del sombrero del primero. El último dice que no sabe de qué color es el suyo. El segundo dice lo mismo, pero el primero, que no ve nada, dice que sí sabe el color del suyo. ¿De qué color es dicho sombrero? Esta es una de las mejores muestras acerca de la cantidad de información que aporta el saber si algo tiene o no solución. |
||||||||||||||||||||||||||||||||
|
Seis copas Colocamos en fila seis copas, de modo que las tres primeras estén llenas y las otras tres vacías. ¿Cómo podemos alternarlas moviendo una sola copa? El secreto de los números, p.59. |
||||||||||||||||||||||||||||||||
|
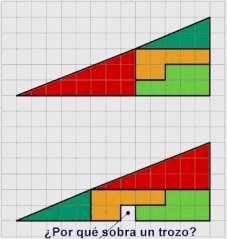
El área desaparecida (Paradoja de Curry)
Yon (1-3-2003) nos propone esta famosa paradoja, inventada por Paúl Curry, un mago aficionado, allá por 1953. La pregunta es: ¿alguien sabe dónde está el cuadrado que falta? Mathematics, Magic and Mystery, p.139. |
||||||||||||||||||||||||||||||||
|
Una ecuación con infinitas equis Se trata de resolver la siguiente ecuación: Una variante interesante es la siguiente: Pista: en otro lugar de Epsilones se hace justo lo contrario a lo que tenemos que hacer aquí. Otra pista: es mucho más fácil de lo que parece. |
||||||||||||||||||||||||||||||||
|
La Torre Eiffel, a escala ¿Sabrías calcular cuanto pesaría una maqueta de la Torre Eiffel construida a escala con exactamente los mismos materiales de medio metro de altura? Te daré algunos datos (por supuesto, no todos son necesarios): entre 1887 y 1889 trescientos montadores ensamblaron los dos millones y medio de remaches de la torre. Su peso total es de 10100 toneladas, siendo inferior que el de una columna de aire de su misma base. Su altura, incluida la antena de televisión, es de 320 metros. Podemos subir a pie gracias a 1652 escalones. La altura oscila unos 15 cm dependiendo de la temperatura. París (La Guía Verde), p.158; web: página oficial de la Torre Eiffel. |
||||||||||||||||||||||||||||||||
|
Un duelo a tres En la literatura los duelos suelen ser entre dos, pero en esta ocasión tenemos tres contendientes: Mr. A, Mr. B y Mr C. Resulta que Mr. A solo acierta una de cada tres y Mr. B dos de cada tres, mientras que Mr. C acierta siempre. Para equilibrar, primero tira A, luego B y luego C. ¿Cuál es la mejor estrategia de A? ¿Disparar a Mr. B o a Mr. C? Aparece en Fermat's last Theorem. Pista: además de disparar a Mr. B o a Mr. C, Mr. A puede optar por una tercera posibilidad. |
||||||||||||||||||||||||||||||||
|
Triángulos y cerillas (II) Dado un triángulo formado con tres cerillas, ¿cómo conseguir ocho triángulos añadiendo solo tres cerillas más y sin mover las anteriores? Nano (27-10-2002), al intentar resolver el problema Triángulos y cerillas (I), ha encontrado una configuración interesante, pero, como es más chulo que nadie, no de cuatro triángulos sino del doble, ¡de ocho! Y lo más genial del asunto es que es muy fácil. |
||||||||||||||||||||||||||||||||
|
Triángulos y cerillas (I) Dado un triángulo formado con tres cerillas, ¿cómo conseguir que sean en total cuatro triángulos iguales al original añadiendo solo tres cerillas más y sin mover las anteriores? The Philosophy of Space & Time, p.41. |
||||||||||||||||||||||||||||||||
|
Triángulos y cerillas (III) En Epsilones ya tenemos dos enunciados con triángulos y cerillas. Vamos por el tercero, enviado por Alfredo Fernández Díaz (2-10-2004): “Dado un triángulo formado con tres cerillas, ¿cómo conseguir seis triángulos añadiendo solo tres cerillas y sin mover las anteriores?” Alfredo nos da una pista: “Encontré la solución en el siglo pasado”. |
||||||||||||||||||||||||||||||||
|
Primos entre sí Se trata de demostrar que si se escogen n + 1 enteros menores o iguales que 2n, al menos dos de ellos son primos entre sí (por ejemplo, si escogemos 7 = 6+1 enteros menores o iguales que 12 = 2·6). Según se cuenta en The Man Who Love Only Numbers, Erdös se lo planteó a un joven genio de doce años que lo resolvió mientras se tomaba la sopa. |
||||||||||||||||||||||||||||||||
|
Una mosca viajera Dos bicicletas que distan 90 Km. parten a la vez la una al encuentro de la otra, una a 10 y la otra a 20 Km./h. Al mismo tiempo, y junto a la primera bicicleta, sale una mosca en su mismo sentido. Cuando la mosca llega a donde se encuentra la segunda bicicleta, da la vuelta y retrocede en busca de la primera. Cuando llega a donde está la primera, da la vuelta y va de nuevo en busca de la segunda. Si la mosca repite este proceso hasta que ambas bicicletas se encuentran, ¿cuál será el espacio recorrido en total por la mosca si esta va a 40 Km./h? Todo un clásico. Pista: apenas hay que hacer cálculos. |
||||||||||||||||||||||||||||||||
|
La fuente y las jarras
Nos encontramos frente a una fuente y disponemos de dos jarras de 3 y 5 litros.¿Cómo podemos conseguir exactamente cuatro litros de agua sin utilizar ningún otro recipiente? Según W.W. Rouse Ball, este tipo de problemas llevan apareciendo en las colecciones de problemas desde la Edad Media. Y solo se pueden resolver probando. Mathematical recreations and Essays, p.27. |
||||||||||||||||||||||||||||||||
|
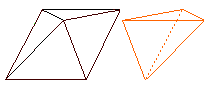
Una pirámide y un tetraedro Al juntar una pirámide de base cuadrada y un tetraedro cuyas caras son iguales que las caras laterales de la pirámide, ¿cuántas caras tiene el sólido resultante? Planteado por Clarke en su novela El espectro del Titanic. |
||||||||||||||||||||||||||||||||
|
Las fichas y el florero Disponemos de infinitas fichas numeradas. A las doce menos un minuto metemos en un florero las fichas que van de la 1 a la 10 y sacamos la 1. Medio minuto antes de las doce metemos de la 11 a la 20 y sacamos la 2. Un tercio de minuto antes de las doce metemos de la 21 a la 30 y sacamos la 3. Y así sucesivamente. ¿Cuántas fichas habrá a las doce en punto en el florero? Nuevos pasatiempos matemáticos, p.163. ► Paradojas de numerabilidad. |
||||||||||||||||||||||||||||||||
|
1 = 0,999999999999999999999999999999999999999999999.... Se trata de demostrar la igualdad Nano (26-10-2002) manda esta cuestión: él ya conoce la demostración que se da en secundaria, pero pide otra que sirva para zanjar una discusión académica. |
||||||||||||||||||||||||||||||||
|
Igualdad de cuadrados de números consecutivos Se sabe que 102 + 112 + 122 = 132 + 142. La cuestión es averiguar si hay alguna otra serie de cinco números enteros consecutivos en la que la suma de los cuadrados de los tres primeros sea igual a la suma de los cuadrados de los otros dos. Luís Gómez, que envío el problema el 10-2-2004, nos explica además su origen en Ejercicio complicado, dentro de la galería de arte de Epsilones. Web: Yakov Perelman |
||||||||||||||||||||||||||||||||
|
A la Luna con una hoja de papel La pregunta es sencilla: ¿cuántas veces tenemos que doblar una hoja de papel para, al aumentar así su grosor, alcanzar la distancia Tierra-Luna? Para ponernos de acuerdo, supondremos que el grosor de la hoja de papel es de 0'1 mm y que la distancia Tierra-Luna es de 384000 km. Almudena (28-4-2003) manda este sencilla cuestión cuya respuesta es, sin embargo, sorprendente. |
||||||||||||||||||||||||||||||||
|
Midiendo fractales ¿Cuál es la superficie del triángulo de Sierpinsky? ¿Cuál es la longitud del Copo de nieve de Koch? Pista: todo lo que hay que conocer es algo acerca de las progresiones geométricas. |
|
Múltiplos de nueve que dan nueve Si cogemos un número múltiplo de 9, sumamos sus cifras, y siempre que el resultado tenga más de una cifra las volvemos a sumar, resulta que finalmente obtenemos un nueve. ¿Por qué?
José (22-9-2004) envía esta cuestión. |
|
Cuatro amigos, la linterna y el puente Cuatro amigos deben cruzar un frágil puente de madera. Es de noche y es indispensable usar una linterna para cruzarlo. El puente sólo puede aguantar el peso de dos personas como máximo y solo tienen una linterna. Alicia tarda 8 minutos en cruzarlo, Benito 4 minutos, Carlos tarda 2 y David 1. ¿Cómo han de cruzar el puente para pasar los 4 al otro lado y tardar el menor tiempo posible en hacerlo? Enviado por Carlota (20-10-2004). |
|
Los colchones de Gulliver "Cuando Gulliver cayó en el pais de los Liliputienses no tenia dónde dormir. Le consigueron 600 colchones. Gulliver era 12 veces mayor proporcionalmente que uno de Liliput. Pregunta: ¿Qué tal durmió aquella noche? (-quitando las recomendaciones médicas de dormir sobre tabla y todo éso...-)" Pista: si no te sale, siempre puedes ver qué hicieron con su comida. Enviado por Rafa Carrique Yribarne (25-12-2004) |
|
Las hijas del Profesor Otto Un colega le pregunta al Profesor Otto las edades de sus hijas y este reponde que el producto de sus edades es igual a 36 y que la suma es igual al número del portal de enfrente. El colega mira el portal en cuestión y, tras pensar un momento, dice que le falta un dato. Entonces el profesor Otto asiente y dice: "La mayor toca el piano". ¿Qué edades tienen las hijas del Profesor Otto? Enviado por Eletema (9-2-2005). He modificado ligeramente el enunciado según la versión que escuché hace muchos, muchos años. Nostalgia senil le llaman. |
|
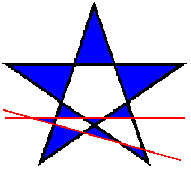
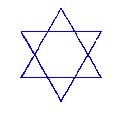
División de la estrella pentagonal en diez triángulos Se trata de dividir una estrella pentagonal en diez triángulos con dos líneas rectas. Los triángulos no deben superponerse. Enviado por Luís (4-1-2005). |
|
Soluciones |
|
Las hijas del Profesor Otto Teniendo en cuenta que el producto de las edades de las tres hijas es 36, las posibilidades, como nos dice Eletema, son las siguientes:
Entonces GaBo, el 15-2-2005, concluye: "Creo que la respuesta es 2-2-9; porque la suma es 13, igual que 1-6-6. El resto de sumas son todas diferentes por lo que si hubiese sido otro resultado no habría sido necesario el dato de saber que la mayor toca el piano. Este último dato nos informa de que existe una mayor con lo que no puede ser 1-6-6 y solo puede ser 2-2-9. Creo que esa es la solución." |
|||||||||||||||||||
|
Los colchones de Gulliver Solución: GaBo dio la solución correcta el 28-12-2004. Los colchones deberán soportar el peso de Gulliver. Dado que Gulliver es doce veces más alto que los Liliputienses, también será doce veces más ancho y más profundo. Es decir, que su volumen, y por tanto su peso, será 123 veces mayor. De aquí se deduce que necesitaremos 123 = 1728 colchones, cifra muy superior a los 600 que se le proporcionan en el enunciado. Conclusión: dormirá fatal el pobre. |
|||||||||||||||||||
|
Cuatro amigos, la linterna y el puente Teano envió la siguiente solución (27-11-2004):
Total: 15 minutos. |
|||||||||||||||||||
|
Múltiplos de nueve que dan nueve Teano envió la siguiente solución (27-11-2004): Una demostración que se me ocurre: Imagínate un número múltiplo de 9: a0 + 10·a1 + 100·a2 + ...+ 10n·an Quieres ver que la suma de todas sus cifras sigue siendo un múltiplo de 9. Usando que si a un múltiplo de 9 le sumas/restas otro múltiplo de nueve el resultado sigue siendo un múltiplo de nueve, sólo tienes que restarle: 9·a1 Y te queda el número a0 + a1 + a2 + ...+ an , que como sale de restar múltiplos de 9 a un múltiplo de 9, será un múltiplo de 9. Si este múltiplo de 9 tiene más de una cifra, vuelves a restar y te volverá a quedar un múltiplo de 9. Hasta que tengas un número que tenga una sola cifra. Y cuando tengas un número con una sola cifra, tendrás un número que será a la vez múltiplo de 9 y a la vez de una cifra. Y solo puede ser el 9. Por tanto, la suma es 9. |
|||||||||||||||||||
|
A la Luna con una hoja de papel Guillermo (16-5-2004) dice: "Sólo hay que resolver la ecuación exponencial 0,0001·2x = 384000000 (después de pasar todo a metros) lo que da como resultado x = 41,80424344. Que habría que doblar la hoja 42 veces, vaya." Está claro: cada vez que doblamos la hoja su grosor se multiplica por dos, por lo que si la doblamos x veces, su grosor se doblará x veces y será, por tanto, 0,0001·2x. Un ejemplo más de crecimiento exponencial. El amigo b4zt4rd, apostilló el 6-2-2005 lo siguiente: "Hola buenas. Acabo de leer el problema de la luna y la hoja de papel en tu Web y quería apostillar una cosa. Ninguna hoja de papel por muy grande que sea puede doblarse más de 7 veces (al menos por un ser humano, no se si una maquina podrá...) por muy grande que sea la hoja. Haz la prueba!! Esto se explica por la relación de Tau=F/S (esfuerzo = fuerza entre superficie). Al aumentar la anchura de la hoja de papel (exponencialmente, como se dice en la solucion del problema) aumentas la superficie sobre la cual se aplica la fuerza, por lo que para realizar el mismo esfuerzo necesitas aplicar una fuerza bestial y es por lo mismo que no puedes romper una baraja de cartas a palo seco y sin embargo es obvio que se pueden romper una a una sin ninguna dificultad... Venga, que vaya bien.." |
|||||||||||||||||||
|
Midiendo fractales Guillermo (16-5-2004) dice: Área del triángulo de Sierpinsky:
como vemos, a cada paso se dividen los triángulos en 4 más pequeños y
se cogen 3, por lo tanto el área de los triángulos negros será de (3/4)n tras n iteraciones. Entonces el área será
Longitud del copo de nieve de Koch:
a cada paso, el segmento se divide en 3 y uno de ellos es sustituido
por 2, así que a cada paso la longitud crece 4/3. La longitud será pues
|
|||||||||||||||||||
|
Los monjes lógicos José Antonio Delgado Castro (3-11-2003) y Franco Basaldella (26-11-2003) mandan la primera de las soluciones: SOLUCIÓN A: Después de hablarles el superior de la orden, los monjes se miran entre sí buscando a las marcas de los elegidos. Si solo fuese uno el elegido, este no vería ninguna marca y sabría por tanto que necesariamente él lo era y marcharía tras la comida. Día 1. Ha pasado un día. Nadie ha marchado, por tanto hay más de uno. Si fueran dos, los elegidos verían solo una marca y sabrían que lo son. Día 2 Nadie ha marchado, por tanto hay más de dos. Si fueran tres, los elegidos verían dos marcas y sabrían que lo son. Día 3 Nadie ha marchado, por tanto hay más de tres. Si fueran cuatro, los elegidos verían tres marcas y sabrían que lo son. Día 4 Nadie ha marchado, por tanto hay más de cuatro. Si fueran cinco, los elegidos verían cuatro marcas y sabrían que lo son. Día 5 Nadie ha marchado, por tanto hay más de cinco. Si fueran seis, los elegidos verían cinco marcas y sabrían que lo son. Día 6 Nadie ha marchado, por tanto hay más de seis. Si fueran siete, los elegidos verían seis marcas y sabrían que lo son. Día 7 Algunos monjes no aparecen: han marchado. Luego ayer supieron que eran los elegidos. Por tanto eran siete. *** Jesús M. Landart a la anterior añade la siguiente: SOLUCIÓN B: Dado que todos los monjes son especialistas en lógica, pueden hacer la reflexión de la solución A desde el primer momento, y concluir que lo que deben hacer es esperar tantos días como marcas ven en las frentes de sus compañeros. Dado que los elegidos ven una marca menos que el resto (la propia), partirán un día antes. Y al día siguiente el resto comprobará que los que quedan son los no elegidos. |
|||||||||||||||||||
|
Nueve puntos Ángeles Carrero nos envía la solución, en la que se ve cómo saliéndose del cuadrado imaginario formado por los nueve puntos podemos resolver el problema:
La cuestión ahora es: ¿se puede mejorar?, es decir, ¿se puede hacer con menos de cuatro segmentos? Pues sí, siempre y cuando consideremos que los puntos no son ideales, es decir, con grosor: en tal caso basta con tres segmentos:
Pero se puede hacer aún mejor: si los puntos están lo suficientemente juntos y el lápiz o lo que utilicemos es lo suficientemente ancho, entonces con un solo trazo (gris en el dibujo) podremos barrer todos los puntos.
Ante tanta solución quizá alguien no sepa decidir cuál es la buena. La cuestión es que todas son igualmente correctas, pues la solución de un problema depende del ámbito en el que el problema se plantea. Este ámbito marca unos límites cuya determinación es muchas veces inconsciente. En el caso que nos ocupa, y sin que nadie nos diga nada, asumimos que los puntos del enunciado son puntos matemáticos, puntos ideales, cuando lo cierto es que en el dibujo del enunciado lo que se pueden ver son circulitos. Pero claro, como estamos en una página de matemáticas, nuestro cerebro está en modo "matemáticas" y tiende a interpretar cuanto ve en los términos habituales de los problemas matemáticos. Otro asunto interesante es el de la primera solución: una vez vista parece completamente trivial, pero contiene un elemento que la hace muy difícil de lograr: se sale del cuadrado imaginario formado por los nueve puntos. ¿Por qué es tan raro que se nos ocurra este "truco"? Según los psicólogos de la Gestalt se debe a lo que llaman principio de cierre, por el cual tendemos a buscar la integridad de las cosas que observamos (en el caso del problema, encerrando a los nueve puntos en un cuadrado imaginario). Conclusiones:
El cerebro creador, p.252; The Quark and the Jaguar, p.270. |
|||||||||||||||||||
|
Alicia en el Bosque del Olvido El jueves. Naturalmente, se puede hallar probando con cada uno de los días de la semana hasta encontrar el que cumple con lo dicho por el león y el unicornio. Sin embargo, la gracia aquí estriba en ir directamente a la solución. Dado que los dos personajes mienten en días distintos, está claro que uno dice la verdad mientras que el otro no. Por tanto, al que dice la verdad le tocaba mentir el día anterior, mientras que al que miente le tocaba decir la verdad el día anterior. De todo ello se deduce que el día pedido es aquel en el que se produce el cambio en la sinceridad de un y otro: el jueves. En cualquier caso, la intuición nos dice que hay que empezar por ahí, ¿verdad? |
|||||||||||||||||||
|
|||||||||||||||||||
|
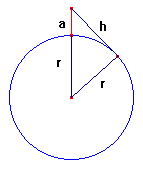
Distancia al horizonte Antes de nada, si no lo has resuelto, te sugeriría que hicieses una estimación a ojo: ¿5 km?, ¿50?, ¿500? Los datos necesarios son el radio de la Tierra, que en el ecuador es de, aproximadamente, 6378 km, y la altura a la que se encuentran los ojos del observador, que podemos situar, dado que estamos en la playa, a unos 2 metros del suelo (0'002 Km.). El horizonte es la línea a partir de la cual no podemos ver más allá a causa de la curvatura de la Tierra. Por tanto, la visual que une nuestros ojos con el horizonte es una línea tangente a la Tierra, y por tanto perpendicular al radio de esta en el horizonte. Esto nos permite, como se puede ver en el esquema, aplicar el teorema de Pitágoras. El observador estaría representado (en nuestro caso playero de un modo evidentemente exagerado) por el segmento rojo.
Basta sustituir a y r por los valores arriba indicados para obtener la solución: h = 5 km. |
|||||||||||||||||||
|
Tres sombreros El razonamiento es sencillo:
Otra forma de decir lo mismo sería la siguiente:
Pese a lo lógica de la solución, en este tipo de problemas se parte de una presunción falsa, y es que tanto A como B como C son perfectos lógicos; sin embargo, no es descabellado pensar que B o C puedan razonar incorrectamente. En tal caso, A podría estar deduciendo con mucha corrección pero a partir de datos falsos, lo cual lleva, casi inevitablemente, al error. Mi abuelo Luciano era un monstruo jugando al dominó. Al poco de empezar una partida sabía perfectamente las fichas que llevaban los demás, siempre y cuando los otros jugadores también fuesen de los buenos. Cuando jugaba con sus nietos se desesperaba, porque lo irracional de nuestras jugadas impedía cualquier deducción. |
|||||||||||||||||||
|
Seis copas Almudena (25-5-2003) y Ángeles Carrero (12-6-2003) nos dan la solución: cogemos la del medio de las tres que están llenas y vaciamos su contenido en la del medio de las que están vacías. Dejamos la copa donde estaba y listo: ya las tenemos alternadas. |
|||||||||||||||||||
|
El área desaparecida (Paradoja de Curry) Christian Viales (27-4-2003) manda esta completa explicación: ***
*** Perfecto. Solo añadiré, para los menos matemáticos, que las dos figuras que se muestran en el problema no son verdaderos triángulos: el de arriba posee una ligera concavidad por el lado mayor (la hipotética hipotenusa), mientras que el de abajo tiene una ligera convexidad, siendo la diferencia entre la convexidad de uno y la concavidad de otro donde se esconde el cuadro desaparecido. Como dice Christian, es el ojo el que nos engaña. |
|||||||||||||||||||
|
Una ecuación con infinitas equis Javier Herrera (10-3-2003) dice:
Para la variante, repitiendo el proceso, se obtienen las soluciones x = 0 y x = 2. |
|||||||||||||||||||
|
La Torre Eiffel, a escala Si r es la razón de semejanza entre la maqueta y la Torre real (r = 0'5/320) entonces la relación entre superficies es r2, y la relación entre volúmenes r3, de donde se tiene que r3 = P / 10100. Despejando, P = 10100·r3 = 0'0000385 Tm, o lo que es lo mismo, 38'5 gramos. Vamos, que una maqueta de medio metro, construida fundamentalmente en hierro, y perfectamente a escala, pesa 38'5 miserables gramos. A eso le llamo yo ligereza. |
|||||||||||||||||||
|
Triángulos y cerillas (I) Nadie nos dice que no podamos salirnos del plano. La solución consiste en colocar las tres nuevas cerillas hacia arriba, formando con las anteriores un tetraedro. |
|||||||||||||||||||
|
Un duelo a tres Resulta que la mejor estrategia es disparar al aire. Entonces B tendrá que disparar a C, que es el oponente más peligroso. Si falla, C entonces le devolverá el disparo, por ser B más peligroso que A, y como es un tirador perfecto, se lo cargará. Total, que uno de los dos, B o C, habrá desaparecido de la competición antes de que el turno le vuelva a A. De esta manera, A modifica la situación para que, en vez de ser el primer tirador de un duelo a tres, lo sea de un duelo a dos. Dejo los detalles (el cálculo de las probabilidades de las tres alternativas) al lector. |
|||||||||||||||||||
|
Primos entre sí La solución (Nano) se basa en dos hechos que por separado son casi triviales: si se escogen n + 1 enteros menores o iguales que 2n resulta que al menos dos de ellos deben ser consecutivos. Por otra parte, dos enteros consecutivos siempre son primos entre sí. Con más detalle, la demostración de Nano dice: 1. Dos números consecutivos son siempre primos entre sí.
2. Tomando n + 1 números menores o iguales que 2n, al menos dos de ellos se diferencian en una unidad.
|
|||||||||||||||||||
|
Una mosca viajera Con este problema uno se suele liar porque empieza a pensar en cómo calcular las distancias que recorre la pobre mosca en cada viaje de ida y vuelta. Pero la verdad es que no hace falta, porque dado que conocemos su velocidad, lo único que necesitamos es saber cuánto tiempo está la mosca en vuelo, y eso es muy fácil. Si una bicicleta va a 10 Km./h y la otra a 20 Km./h y distan 90 Km., ¿cuánto tardarán en encontrarse? Evidentemente: tres horas. Pues ese es el tiempo de vuelo de la mosca. Así que, dado que va a 40 Km./h, en total recorrerá 120 km. (Ver anécdota de von Neumann). |
|||||||||||||||||||
|
La fuente y las jarras Hay muchas posibilidades. Aquí va una de ellas. Por claridad, vamos a llamar J3 a la jarra de tres litros y J5 a la de 5 litros.
Si tienes una solución mejor, mándamela. Y piensa que cuando se dice "mejor" podemos referirnos a dos cosas distintas: menor número de pasos o menor consumo de agua. Otra solución es la que manda Paula Fernández Cándano (18-12-2003):
Más pasos, pero ahorramos agua. ¡Estupendo! A Lorena (15-7-2004) le extrañó el comentario de Rouse Ball de que estos problemas "solo se pueden resolver probando", razón por la que escribió lo siguiente: "Se me ocurre una forma de resolver cualquier problema de este tipo con un procedimiento riguroso (aunque no demasiado directo). La idea es representar la situación en un grafo, donde cada nodo represente un posible estado de las jarras, es decir, los nodos representan pares (n3, n5), donde n3=0,1,2,3 (posible contenido de la jarra de 3 litros) y n5=0,1,2,3,4,5 (posible contenido de la jarra de 5 litros). En este caso, se tienen 24 nodos. El arco dirigido v1 -> v2 estará en el grafo si de la situación representada por el nodo v1 se puede pasar a la situación representada por el nodo v2 en una sola operación (ejemplos de operación : vaciar una jarra a la fuente, volcar todo el contenido de una en otra, llenar una tomando agua de la fuente, etc...). Por ejemplo, estarán en el grafo los arcos: (0,0)-> (0,5), (0,0)->(3,0), (3,0)->(3,5), etc, pero no estarán arcos como: (0,0)->(1,0), (3,5)->(2,5), (0,0)->(3,5). "Luego el problema se reduce a encontrar un camino en el grafo desde el nodo (0,0) al nodo (0,4). Existen algoritmos muy conocidos para encontrar un camino entre dos nodos de un grafo. Algoritmos determinísticos, por lo que se puede encontrar el camino sin necesidad de "probar". "Por supuesto, este procedimiento es generalizable a cualquier cantidad de jarras, de cualquier capacidad, para obtener una dada cantidad de líquido... "¿Te parece?" *** Mi contestación: "Tu solución general al problema de las jarras me parece perfecta. Y la discrepancia con el comentario de Rouse Ball creo que no es más que aparente. Supongo, y digo supongo porque en su texto no da más explicaciones, que cuando habla de trial (que yo he traducido por probar), no excluye que la búsqueda se pueda sistematizar y convertir por tanto en un algoritmo. "Te pondré un ejemplo: si dada una figura queremos encontrar otra congruente con ella de entre las contenidas en un saco, podemos hacerlo con el siguiente algoritmo: se coge una figura de la bolsa y se compara con la inicial. Si coincide, hemos terminado, y si no, apartamos la figura no coincidente y probamos con la siguiente. Con este ejemplo algo simplista pretendo mostrar que un algoritmo puede consistir en probar." |
|||||||||||||||||||
|
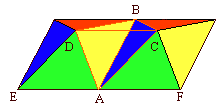
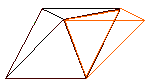
Una pirámide y un tetraedro Podríamos hacer uso de artillería pesada y liarnos con la trigonometría, pero vamos a resolver el problema con argumentos más visuales: en vez de una única pirámide, imaginemos dos, una junto a la otra (ver figura), y pensemos en el sólido necesario para "llenar" el hueco que hay entre ambas, el tetraedro ABCD.
Conclusión: el sólido resultante tiene cinco caras, las mismas que la pirámide original:
|
|||||||||||||||||||
|
Las fichas y el florero Pues ninguna. El razonamiento es el siguiente: pensemos en una ficha en concreto, por ejemplo la 1246. ¿Estará en florero a las doce en punto? No, pues 1/1246 de minuto antes de las doce la sacamos del florero. Esto mismo nos lo podemos preguntar para cualquiera de nuestras infinitas fichas numeradas. ¿Estará la ficha marcada con el número n? No, no estará, porque la habremos sacado cuando faltaba 1/n de minuto para las doce. Conclusión: el florero se queda vacío. Las cosas del infinito. |
|||||||||||||||||||
|
1 = 0,999999999999999999999999999999999999999999999.... 1. Primero, la de secundaria, que no creo necesite más explicaciones:
2. Esta otra demostración tiene de interesante que muestra cómo se pueden entender los desarrollos decimales infinitos como sumas infinitas: Sea la sucesión de término general an = 0,9·0,1n-1, que es una progresión geométrica de razón 0,1 cuyos primero términos son 0,9, 0,09, 0,009, 0,0009... Entonces podemos escribir: Se sabe que la suma infinita de una serie
geométrica de razón menor que uno se obtiene mediante la fórmula (To Inifnity and Beyond, p.32) |
|||||||||||||||||||
|
Igualdad de cuadrados de números consecutivos Tenti (4-3-2004) dice: Sean a-2, a-1, a, a+1, a+2 los 5 números consecutivos: (a-2)2 + (a-1)2 + a2 = (a+1)2 + (a+2)2 Quitando paréntesis y reduciendo términos: a2 - 12a = 0 , de donde se obtiene a = 0, a = 12. Las soluciones son 10, 11, 12, 13, 14 (la dada) y -2, -1, 0, 1, 2. |
|||||||||||||||||||
|
Café: ¿solo o con leche? Mefistófeles (11-6-2004) y G. Alberto (25-6-2004) mandaron la solución correcta. La idea es sencilla: la pérdida de calor se produce a través de las paredes del recipiente, de modo que depende de la superficie de éste. Por otra parte, la cantidad de calor que posee el líquido contenido en el recipiente depende de su masa y, por tanto, de su volumen. Ahora bien: si r es la razón de semejanza entre dos objetos (las medidas lineales de uno son r veces mayores que las del otro), entonces la relación entre sus superficies es r2, mientras que la relación entre sus volúmenes es r3 (ejemplo: si una taza tiene un diámetro y una altura dobles que otra, su superficie será cuatro veces mayor, mientras que su volumen lo será ocho veces). Total: que si las formas son semejantes el volumen crece en mayor proporción que la superficie, lo que significa en nuestro caso que aumenta más la cantidad de calor que la capacidad de perderlo: por eso se enfría antes el líquido de la taza pequeña. (Para los más físicos: la ley de enfriamiento de Newton dice que |
|||||||||||||||||||
|
Veinte panes para veinte personas La solución, aportada por Cheque_Soto (12-7-2004) y PepeMaster (15-8-2004), es la siguiente: Sea x el número de hombres, y el número de mujeres y z el número de niños. Entonces se tiene:
Despejando,
Dado que hablamos de personas, x, y y z deben ser naturales, por lo que z debe cumplir las siguientes condiciones:
Si z es par, z ≥ 14 y z ≤ 16, z solo puede tomar los valores 14 y 16, lo que da las dos posibilidades siguientes: A)
B)
El considerar buena o no la solución B es una cuestión opinable, aunque el enunciado parece dar por sentado que había hombres, mujeres y niños. |
|||||||||||||||||||
|
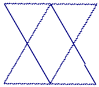
Triángulos y cerillas (III) Un comunicante anónimo dice (9-10-2004): "Dado el triángulo equilátero inicial formado por las tres cerillas, colocas las otras tres en forma de triángulo mirando para abajo con la punta inferior en el punto medio del lado del otro triángulo. Como una estrella de David (donde con el mismo enunciado podríamos hacer 8 triángulos) pero donde la punta inferior del triángulo inverso coincide con el lado inferior del otro triángulo." En este caso, nada mejor que una imagen:
|
|||||||||||||||||||
|
Las tres llaves de luz La solución la mandó Enrique (Kikegall) el 31-3-2005. Cerramos dos de los interruptores durante un tiempo, y luego abrimos uno de los dos que hemos cerrado. Subimos al tercer piso y observamos:
|
|||||||||||||||||||
|
El número de espectadores Sea x el número de espectadores. Que "el 15,555... % de los espectadores estaban en el graderío sur" quiere decir que "el 15,555... % de los espectadores" es un número natural. Entonces el 15,555... % de x = x·15,555.../100 es natural. (1) Ahora expresamos 15,555.../100 como fracción irreducible: se tiene: 15,555.../100 = 7/45. Por (1), x·7/45 es natural, de donde se deduce que x es divisible entre 45. Repitiendo el razonamiento con 24,524524..., que tiene por fracción generatriz irreducible 245/999, x es divisible entre 999. Si x es divisible entre 45 y 999 también lo es entre el mínimo común múltiplo de 45 y 999, que es 4995. Como se dice que "el campo estaba prácticamente lleno" hay que pensar entonces que x es el múltiplo de 4995 más cercano por defecto a 25000. Basta pues hacer la división entera 25000/4995, que da 5, y multiplicar 4995 por 5 para tener el número de espectadores: 24975. |
|||||||||||||||||||
|
La reflexiva sobra Pues no, claro. Lo que pasa es que en la presunta demostración hay un error. Vamos a repetirla para ver dónde: Si aRb entonces, por la simétrica, bRa Como aRb y bRa, por la transitiva, aRa. Pero esto solo es cierto, y por eso he subrayado el "si" condicional de la línea anterior, si dado a existe un b tal que aRb. Pero si a es un elemento que no está relacionado con ningún otro, entonces la simetría y la transitividad no nos pueden asegurar que aRa, y por tanto no podemos afirmar la reflexividad de R. En cualquier caso, no deja de ser interesante observar que la simetría y la transitividad más la condición de que cada elemento esté relacionado con al menos un elemento del conjunto (puede ser él mismo o no) implican la reflexividad. |
|||||||||||||||||||